Daftar Isi

Cakupan Pelatihan

Dalam modul ini, kita akan mempelajari hal berikut:

Pemrosesan data variabel lingkungan
Pemodelan distribusi spesies dengan metode
- Maximum Entropy (MaxEnt)
- Generalized Linear Modeling (GLM)
- Occupancy Modelling

Alat yang digunakan untuk pelatihan ini serta tautan untuk mengunduhnya:

Bahasa pemrograman R https://cran.r-project.org/ dan RStudio https://www.rstudio.com/products/rstudio/download/
MaxEnt https://biodiversityinformatics.amnh.org/open_source/maxent/

Data yang digunakan untuk pelatihan ini merupakan data hasil survei camera trap di Intensive Protection Zone (IPZ) Taman Nasional Bukit Barisan Selatan (TNBBS) sehingga tidak dapat dibagikan secara terbuka. Namun, pengguna modul dapat menggunakan sumber data species occurrence lain dengan penyesuaian tertentu agar script dapat bekerja, salah satunya camera trap mock data yang dapat diunduh dari https://bit.ly/modulCT. Modul ini lebih menekankan pada bagaimana menjalankan pemodelan, bukan penjelasan teoretis pemodelan distribusi spesies.

Prasyarat

Modul ini dibuat dengan asumsi bahwa pengguna modul sudah memiliki pengetahuan dan keterampilan mendasar tentang hal berikut:

Sistem Informasi Geografis
- Perbedaan data vektor (point, line, dan polygon) dan data raster
- coordinate reference system (CRS)
- Transformasi data spasial
Bahasa Pemrograman R
- Pengelolaan working directory
- Tipe-tipe objek di R
- Statistika dasar
- Visualisasi data dengan base R dan package ggplot2
- Transformasi data dengan perintah filter, subset, arrange, select, mutate, group_by, summarise
Pengelolaan dan Analisis Data Camera Trap
- Komponen data camera trap
- Trap nights, capture rate, dan relative abundance index (RAI)

Pendahuluan

Berdasarkan Rondinini et al. (2006), representasi keberadaan spesies dalam ruang dapat dikategorikan menjadi tiga:

Point locality, yaitu titik keberadaan spesies yang berasal dari observasi di lapangan atau koleksi spesimen.
Geographic range, yaitu batas eksternal distribusi spesies. Peta distribusi spesies di halaman IUCN merupakan contoh dari geographic range.
Predicted distribution models, yaitu distribusi spesies yang diprediksi berdasarkan hubungan antara spesies dan faktor-faktor lingkungan. Terdapat dua macam predicted distribution models:
- Deductive Distribution Models
  Hubungan spesies-habitat diperoleh dari literatur dan pengetahuan ahli (expert-based). Contoh model distribusi spesies deduktif adalah model kesesuaian habitat >5000 spesies mamalia di dunia yang dilakukan oleh Rondinini et al. (2011). Model tersebut dibuat dengan mengumpulkan pengetahuan ahli tentang karakteristik habitat yang disukai spesies dari website IUCN (iucnredlist.org), kemudian preferensi habitat spesies tersebut dipetakan berdasarkan tipe tutupan lahan, elevasi, dan fitur hidrologi. Metode ini kurang akurat dibandingkan metode induktif, tetapi efektif dilakukan jika spesies yang akan dimodelkan banyak (ribuan), data koordinat keberadaan spesies tidak tersedia untuk sebagian besar spesies, dan berskala regional atau global.
- Inductive Distribution Models
  Hubungan spesies-habitat disimpulkan dari kondisi habitat tempat spesies ditemukan. Istilah species distribution modeling biasanya digunakan untuk merujuk pada proses atau metode pembuatan peta distribusi induktif.
  Metode ini lebih akurat dibandingkan dengan metode deduktif karena menggunakan titik koordinat keberadaan spesies. Namun, tidak efektif untuk memodelkan banyak spesies.

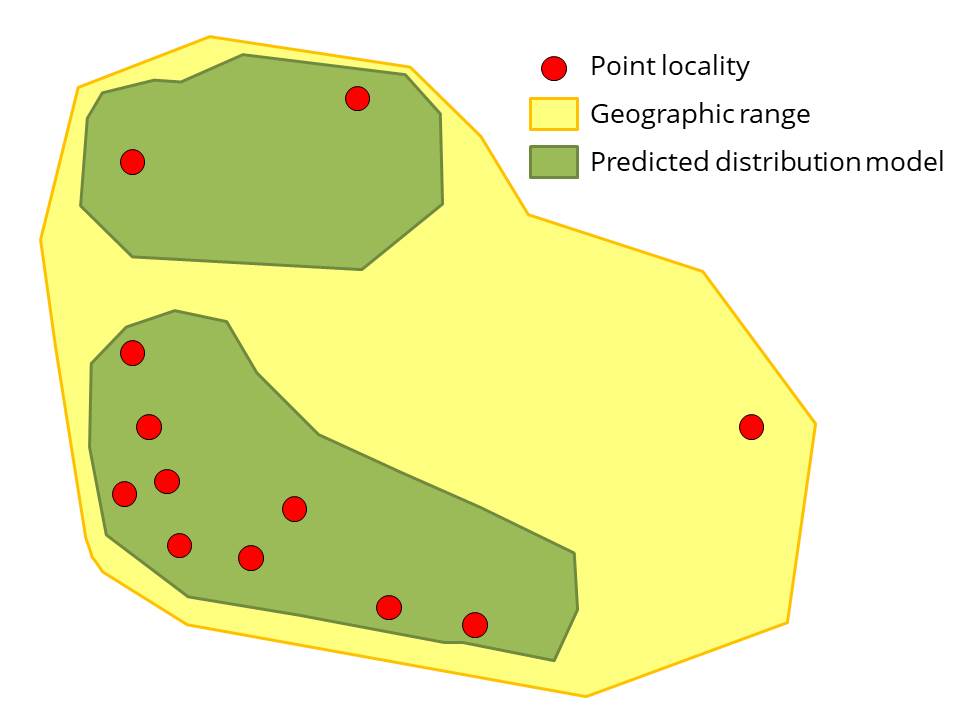
Gambar 1. Representasi keberadaan spesies dalam ruang

Species Distribution Modelling merupakan metode untuk memprediksi distribusi spasial spesies sebagai suatu fungsi terhadap variabel-variabel lingkungan. Secara umum, SDM terbagi menjadi dua kategori berdasarkan metode komputasinya:

Statistical Models
Metode ini menggunakan framework statistik, pada umumnya berbasis regresi linier, untuk memodelkan hubungan spesies-habitat. Contoh metode statistik untuk melakukan SDM adalah generalized linear model (GLM), generalize additive model (GAM), multivariate adaptive regression splines, dan occupancy modeling.
Machine Learning
Metode ini merupakan pemodelan distribusi spesies menggunakan algoritma komputer yang mampu meningkatkan kemampuan prediksi model secara otomatis berdasarkan “pengalaman” atau bertambahnya data. Contoh metode: maximum entropy (Maxent) dan artificial neural network.

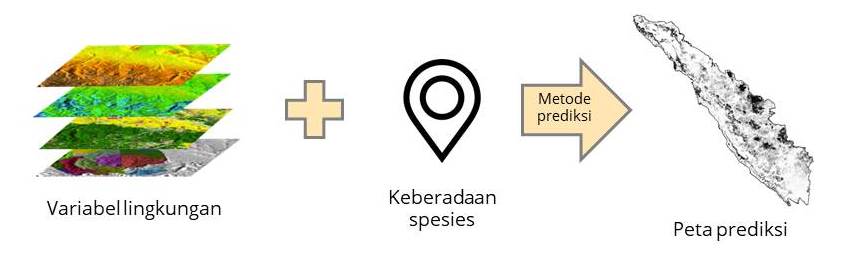
Gambar 2. Proses pemodelan distribusi spesies

Hal pertama yang perlu dilakukan untuk membuat pemodelan distribusi spesies adalah membuat konsep. Pertanyaan-pertanyaan arahan yang dapat digunakan antara lain:

Spesies apa yang akan dimodelkan?
Apa sumber daya yang digunakan spesies untuk bertahan?
Faktor apa saja yang membatasi pertumbuhan populasi spesies?
Gangguan manusia apa yang memengaruhi kesintasan spesies?
dsb.

Pertanyaan-pertanyaan ini dapat membantu kita dalam menentukan variabel lingkungan yang akan dipakai dalam pemodelan. Setelah membuat konsep pemodelan, tahap selanjutnya adalah persiapan data, yaitu:

Variabel lingkungan (disebut juga prediktor atau kovariat)
Data keberadaan spesies
- Maxent: species presence
- GLM: species presence dan absence
- Okupansi: detection dan non-detection

Biasanya, tahap inilah yang memakan paling banyak waktu proses pemodelan, bahkan bisa mencapai > 50% total waktu.

Bentuk data keberadaan spesies berbeda untuk setiap metode sehingga akan dibahas pada setiap bab metode pemodelan. Namun, variabel lingkungan yang akan digunakan hampir sama sehingga akan dibahas terlebih dahulu.

Pemrosesan Variabel Lingkungan

Untuk menentukan variabel lingkungan apa saja yang akan digunakan untuk pemodelan, kita harus mengetahui ekologi spesies yang akan dimodelkan dan skala pemodelan. Misalnya, jika kita ingin memodelkan satwa arboreal seperti siamang, faktor utama yang penting bagi keberadaannya adalah struktur tajuk pohon yang memungkinkan mereka bergerak dan sumber pakan, yaitu buah dan daun pohon di hutan primer atau sekunder. Oleh karena itu, kita dapat mengasumsikan bahwa data spasial yang memengaruhi keberadaannya adalah data yang terkait kualitas habitat hutan, misalnya persentase tajuk hutan, tutupan lahan hutan primer dan sekunder, jarak dari tepi hutan, dan NDVI. Namun, jika spesies yang akan dimodelkan adalah tumbuhan, mungkin faktor lingkungan terkait iklim, cuaca, dan tanah lebih berpengaruh, misalnya curah hujan tahunan, suhu minimal dan maksimal, dan komposisi tanah.

Selain sumber daya, variabel lingkungan lain yang dapat memengaruhi keberadaan satwa adalah gangguan manusia. Hal ini dapat direpresentasikan sebagai pengaruh langsung, misalnya tutupan lahan perkebunan dan permukiman sebagai nonhabitat (tergantung spesiesnya), maupun secara tidak langsung, misalnya kita asumsikan jarak dari jalan sebagai proksi terhadap perburuan dan perambahan.

Data spasial yang akan digunakan sebagai prediktor lingkungan dalam pemodelan distribusi spesies harus memiliki extent, resolusi, dan CRS yang sama. Beberapa metode transformasi data spasial yang sering digunakan untuk pemrosesan prediktor lingkungan adalah:

Convert vector to raster
Digunakan jika data dasar yang digunakan dalam format vektor sehingga perlu dikonversi menjadi raster
Contoh: tutupan lahan
Resample
Digunakan data dasar sudah dalam raster, tetapi extent, resolusi, atau CRS belum sama
Contoh: elevasi, NDVI
Terrain analysis
Untuk memperoleh data turunan dari Digital Elevation Model (DEM)
Contoh: kelerengan (slope), keterjalan tapak (roughness)
Euclidean distance
Untuk memperoleh jarak ke suatu fitur
Contoh: jarak ke tepi hutan, jarak ke pemukiman, jarak ke sungai

Data Latihan

Untuk praktik ini, kita akan menggunakan lima variabel lingkungan, yaitu elevasi, kemiringan lereng (slope), keterjalan tapak (roughness), NDVI, dan jarak dari tepi hutan. Sebelumnya, kita perlu memasang package yang akan digunakan untuk membuat raster variabel lingkungan dengan perintah install.packages(c("rgdal","rgeos","sp","raster","tidyverse")). Jika sudah terpasang, aktifkan package tersebut dengan perintah library

library(rgdal);library(rgeos);library(sp);library(raster);library(tidyverse)

Cetakan Area Studi

Tahap selanjutnya adalah menentukan cakupan area pemodelan yang akan dijadikan sebagai cetakan atau acuan extent, resolusi, dan CRS saat membuat raster variabel lingkungan. Kita dapat menggunakan batas administrasi kawasan studi untuk hal ini.

Jika area studi adalah pulau, batas ekologis distribusi spesies jelas karena area daratan dibatasi oleh laut. Namun, jika area studi adalah buatan manusia, seperti kawasan taman nasional atau cagar alam yang dikelilingi oleh fitur daratan juga, spesies dapat bergerak keluar dari batas kawasan sehingga kita perlu membuat buffer batas kawasan. Jarak buffer untuk SDM tidak ada ketentuan khusus. Intinya, kita hanya ingin melihat prediksi distribusi spesies di sekitar batas kawasan dan buffer ini tidak memengaruhi hasil prediksi (berbeda dengan analisis SECR di mana jarak buffer berpengaruh terhadap estimasi kepadatan satwa). Jarak sejauh 3-10 km sudah cukup.

Jika terdapat bagian kawasan yang berbatasan langsung dengan badan air, misalnya danau besar atau laut, bagian tersebut perlu dipotong karena merupakan nonhabitat. Hal sebaliknya berlaku jika spesies yang kita kaji spesies akuatik.

Kemudian, kita perlu menentukan resolusi template raster. Resolusi untuk semua variabel lingkungan sebaiknya berdasarkan variabel lingkungan yang data aslinya berformat raster dan resolusinya paling besar. Misalnya diketahui ada dua variabel, yaitu elevasi beresolusi 90x90m dan citra landsat dengan resolusi 30mx30m. Resolusi yang digunakan adalah 90mx90m. Raster dengan resolusi lebih kecil dapat di-resample ke resolusi yang lebih besar dengan dirata-ratakan. Namun, men-scale down raster ke resolusi yang lebih kecil tidak dianjurkan.

Data yang akan kita gunakan pada latihan ini yang resolusinya paling besar adalah data elevasi (90mx90m). Idealnya, kita memakai resolusi ini, tetapi semakin kecil resolusi, semakin banyak jumlah petak (grid/cell) raster yang akan diproses sehingga waktu pemrosesan akan lebih lama. Perbedaan waktunya bisa selama beberapa jam hingga beberapa hari, tergantung besar area studi. Untuk efisiensi waktu, dalam latihan ini kita akan memakai resolusi 250x250m. Resolusi ini sebenarnya juga dapat digunakan untuk penelitian atau publikasi di jurnal ilmiah asalkan cakupan area studinya cukup besar, misalnya satu taman nasional. Namun, jika area studi kecil, seperti Stasiun Penelitian Way Canguk yang luasnya 800 hektar, resolusi ini terlalu besar.

Dalam contoh ini, kita akan memakai menggunakan batas Taman Nasional Bukit Barisan Selatan dan membuat buffer sejauh 5 km.

# CRS yang akan digunakan
utm48s <- CRS("+proj=utm +zone=48 +south +datum=WGS84 +units=m +no_defs")
wgs <- CRS("+proj=longlat +datum=WGS84 +no_defs")

# Batas kawasan TNBBS, data sudah dalam UTM
bbs <- readOGR("Input Data/bbs_dissolve2.shp")

# Batas daratan Pulau Sumatera, data dalam geographic CRS
sumatra <- readOGR("Input Data/Sumatra_main-island.shp")

# Mengubah CRS sumatra menjadi UTM 48S
sumatra <- spTransform(sumatra, utm48s)

# Membuat buffer. Keluaran berformat vektor
bbsbuffer <- buffer(bbs, width=5000) #  width dalam satuan meter

par(mar=c(1,1,1,1))
plot(bbsbuffer, col="green"); plot(bbs, add=T); plot(sumatra, add=T)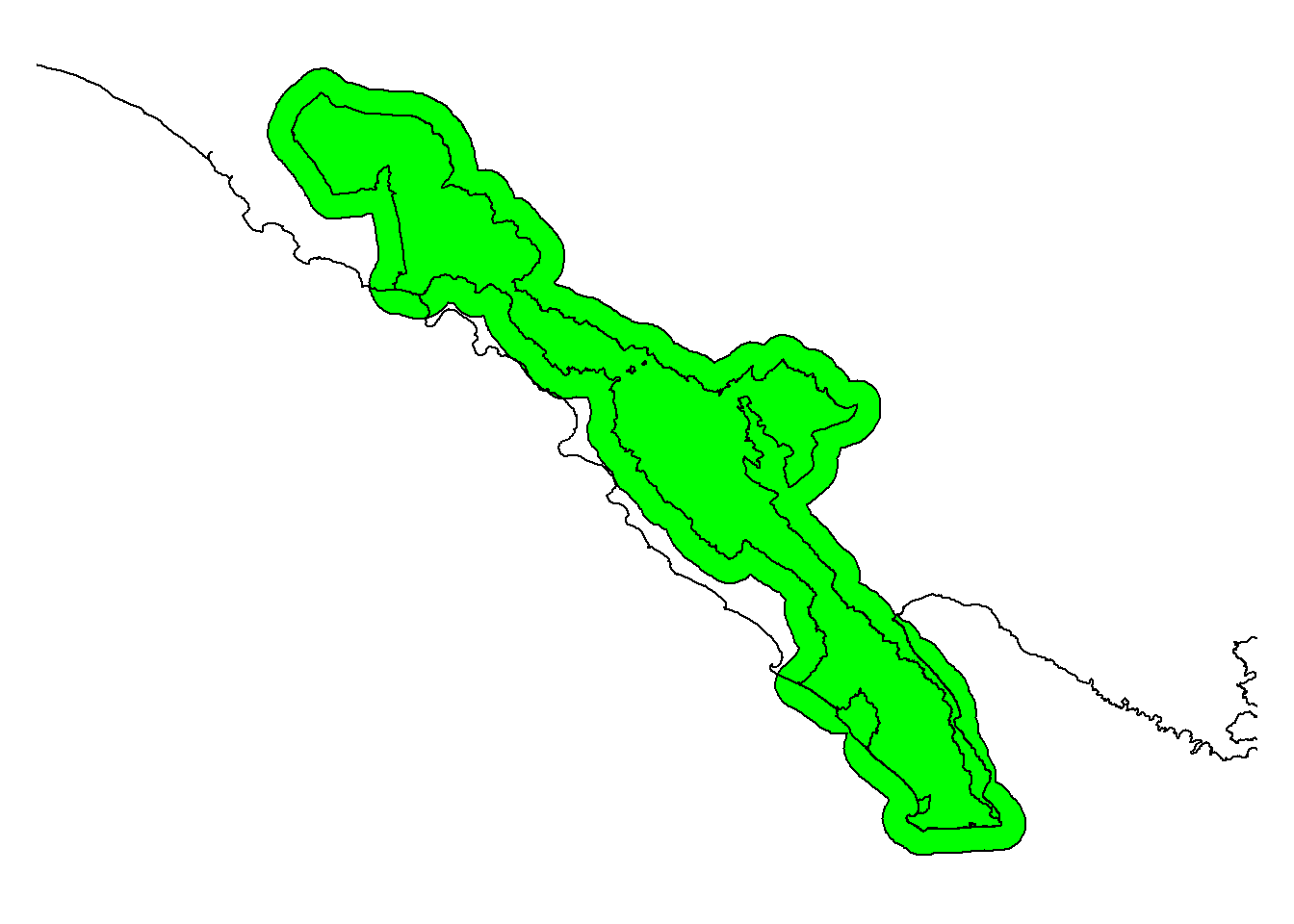

Nah, ada bagian cetakan yang masuk ke laut sehingga perlu dipotong menggunakan batas daratan Pulau Sumatera.

# Memotong area yang masuk ke laut
bbsbuffer <- raster::intersect(bbsbuffer,sumatra)

plot(bbsbuffer, col="green"); plot(bbs, add=T); plot(sumatra, add=T)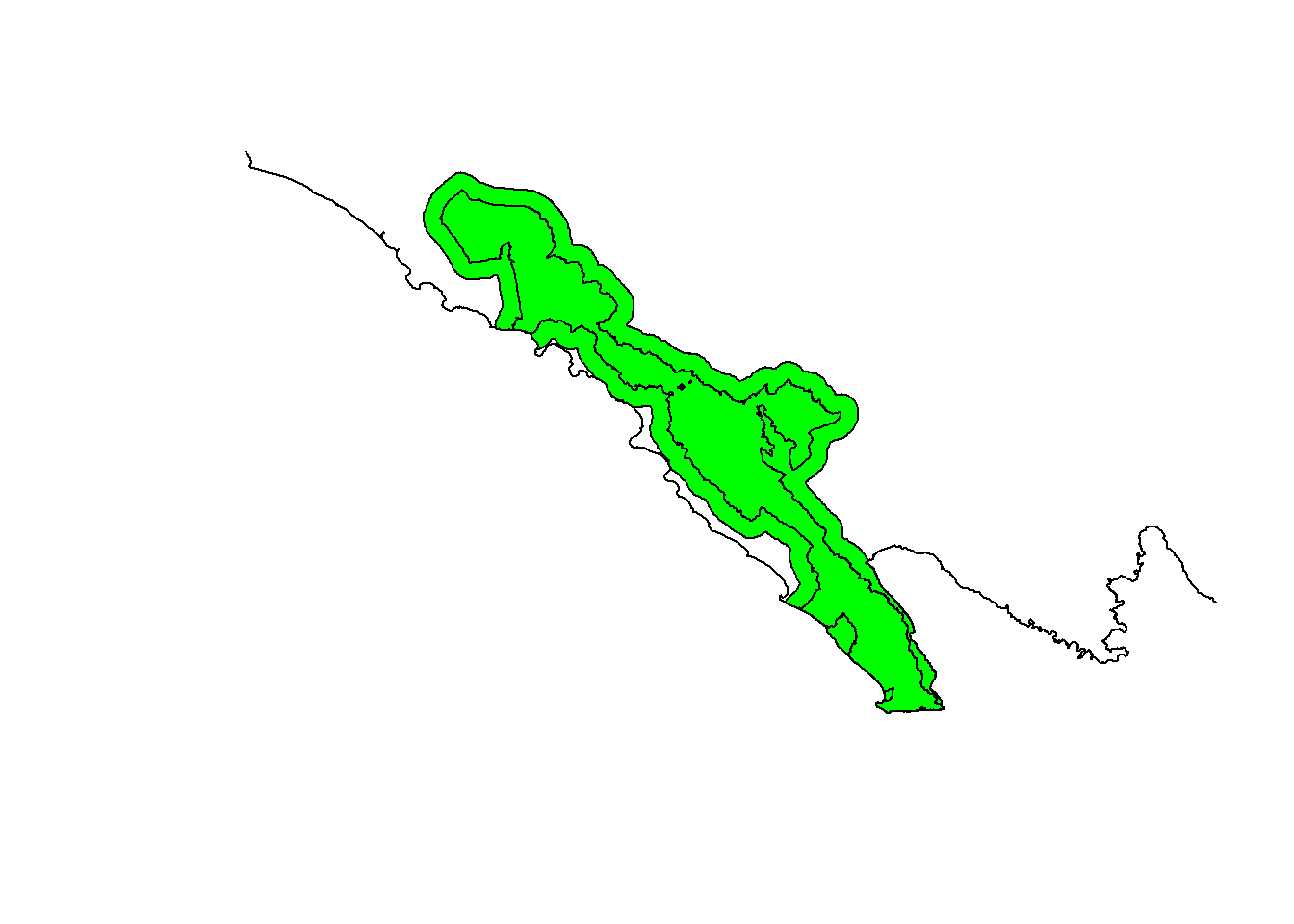

Hasil dari proses di atas adalah vektor poligon sehingga perlu kita konversi menjadi raster. Kita akan menggunakan extent dari bbsbuffer, resolusi 250mx250m, dan CRS UTM zona 48S. Sel raster diberikan nilai 0.

# Konversi menjadi raster
bbstemp <- raster(vals=0,ext=extent(bbsbuffer),resolution=c(250,250),crs=utm48s)

1. Elevasi

Data elevasi yang digunakan adalah Shuttle Radar Topographic Mission (SRTM) 90m Digital Elevation Model yang dapat diperoleh dari https://cgiarcsi.community/data/srtm-90m-digital-elevation-database-v4-1/. Data SRTM juga tersedia dalam resolusi yang lebih kecil, yaitu 30m, yang dapat diunduh dari https://earthexplorer.usgs.gov/, tetapi untuk latihan ini, kita akan memakai yang 90m.

Pertama, kita akan memanggil data elevasi ke R dengan perintah raster. Data yang asli sebenarnya berupa petak-petak berukuran sekitar 520kmx520km dan bisa saja area penelitian kita mencakup lebih dari satu petak SRTM. Supaya lebih praktis, petak-petak SRTM di Pulau Sumatera sudah saya gabungkan menjadi satu raster Sumatra_srtm90m.tif.

# Memanggil data elevasi
elesumatra <- raster("Input Data/Sumatra_srtm90m.tif")

# Resample elevasi ke template raster dengan CRS UTM 48S dan resolusi 250m
ele <- projectRaster(from=elesumatra,to=bbstemp)

Raster mencakup seluruh extent bbstemp sehingga kita perlu memotongnya menggunakan poligon bbsbuffer

# Sebelum dipotong
plot(ele)

# Memotong raster dengan batas poligon bbsbuffer
ele <- mask(ele, bbsbuffer)

# Setelah dipotong
plot(ele)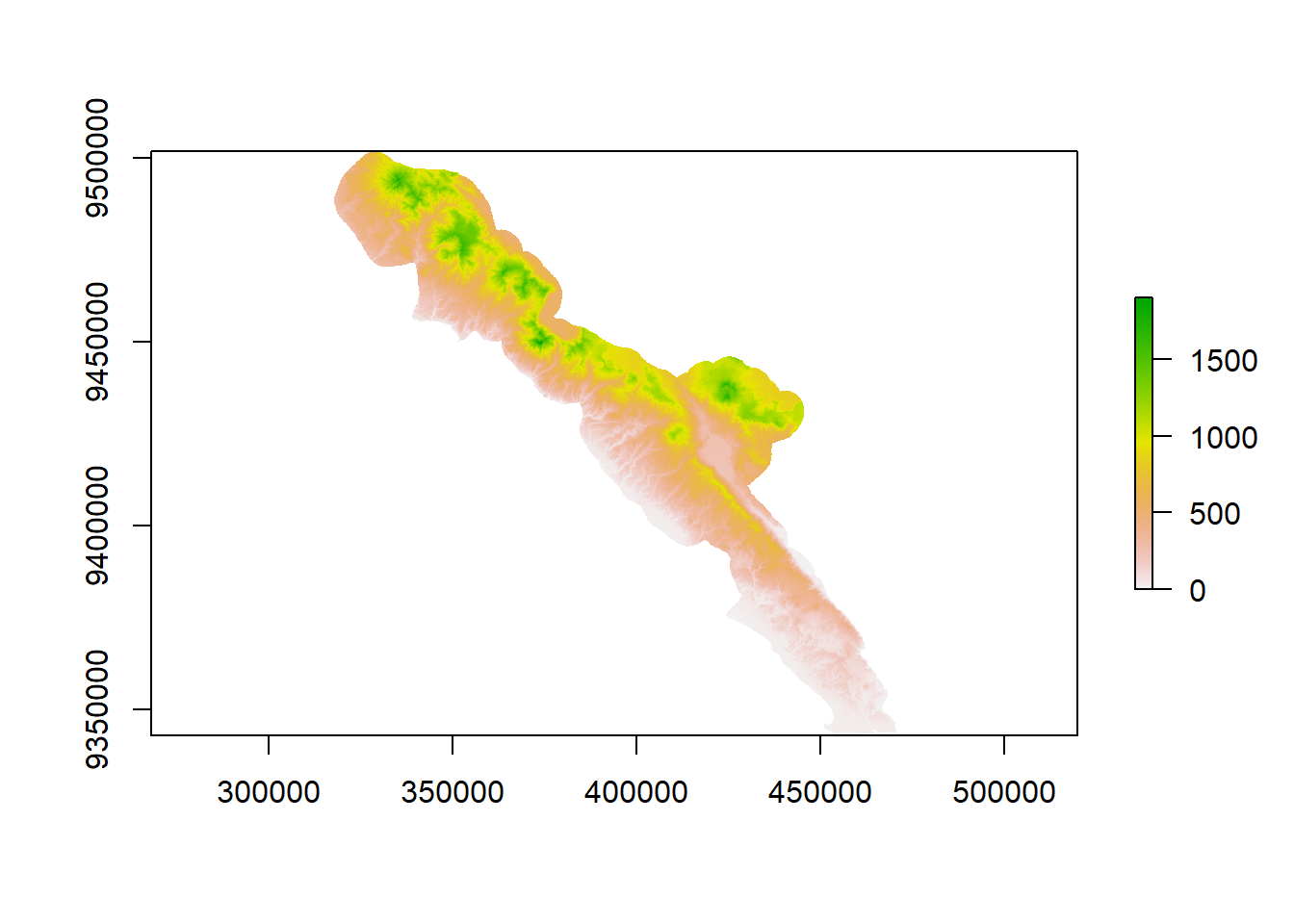

Kemudian kita menulis raster ke dalam format .asc (wajib untuk Maxent) di folder bernama Predictors di working directory kita. Buat folder Predictors terlebih dahulu sebelum menjalankan perintah di bawah ini.

# Ekspor raster
writeRaster(ele, "Predictors/res250m_elevation.asc")

# Hapus elesumatra agar tidak memenuhi memori
rm(elesumatra)

2. Kemiringan lahan (slope) dan keterjalan tapak (roughness)

Slope dan roughness merupakan data turunan yang dibuat dari data elevasi menggunakan fungsi terrain analysis.

# Slope
slo <- terrain(ele, opt="slope", unit="degrees")
writeRaster(slo, "Predictors/res250m_slope.asc")

# Roughness
rou <- terrain(ele, opt="roughness")
writeRaster(rou, "Predictors/res250m_roughness.asc")

3. NDVI

Normalized difference vegetation index (NDVI) adalah indeks yang menguantifikasi kepadatan vegetasi berdasarkan spektrum cahaya near-infrared (NIR), yang dipantulkan tumbuhan, dan spektrum cahaya merah (R), yang diserap oleh tumbuhan. NDVI berkisar antara -1 (tidak ada tumbuhan, misalnya badan air) hingga +1 (kepadatan vegetasi tinggi). NDVI dihitung dengan menggunakan nilai reflektansi spektrum cahaya pada vegetasi dari citra satelit multispektral. Berikut adalah rumus untuk kalkulasi NDVI: \[\text{NDVI }=\displaystyle \frac{(\text{NIR }-\text{ R})}{(\text{NIR }+\text{ R})}\]

Nilai band NIR dan merah dapat diperoleh dari citra satelit Landsat, tetapi jika area studi luas, biasanya akan terdapat “lubang” awan. Namun, kita dapat menggunakan citra Landsat tahun 2019 bebas awan oleh Hansen et al. (2013) yang dapat diunduh dari https://earthenginepartners.appspot.com/science-2013-global-forest/download_v1.7.html. Berdasarkan website tersebut, diketahui bahwa citra terdiri dari empat band, yaitu:
- Layer 1: Band 3 (merah)
- Layer 2: Band 4 (NIR)
- Layer 3: Band 5 (Short-Wave Infrared/SWIR)
- Layer 4: Band 7 (SWIR)
Jadi, kita akan memakai layer pertama (merah) dan kedua (NIR).

Karena satu petak data besar dan akan memakan waktu yang lama jika kita run dari R, dalam latihan ini, kita akan menggunakan data yang sudah dipotong.

# Panggil data
landst <- brick("Input Data/Hansen_GFC-2019-v1.7_last_00N_100E_clipped.tif")

# Resample data Landsat ke template raster
landst <- projectRaster(from=landst, to=bbstemp) 
# harap bersabar karena agak lama

# Plot
landst  <- mask(landst , bbsbuffer)

# Hitung NDVI
ndv <- (landst[[2]] - landst[[1]]) / (landst[[2]] + landst[[1]])
# angka di dalam kurung kotak menunjukkan urutan nomor layer

# Ekspor raster
writeRaster(ndv, "Predictors/res250m_ndvi.asc")

4. Jarak dari tepi hutan

Jarak dari tepi hutan bernilai 0 jika lokasi berada di luar hutan atau tepat di tepi hutan. Nilai semakin tinggi jika lokasi berada di interior hutan. Untuk mendapatkan variabel ini, kita membutuhkan peta tutupan lahan yang dapat diperoleh dari webgis KLHK. Namun, karena data tutupan lahan ini nasional, biasanya kurang akurat untuk dipakai dalam skala lokal, misalnya satu lokasi TNBBS.

Khusus di TNBBS, telah tersedia data tutupan lahan yang dibuat dari data Landsat dan diklasifikasi menggunakan metode kombinasi antara Maximum Likelihood Classification (MLC) dan interpretasi secara visual (Lubis et al. 2018). Kita akan memakai data tersebut untuk mengukur jarak dari tepi hutan ke interior hutan.

Data tutupan lahan TNBBS berupa data vektor poligon yang terdiri dari 13 kategori tutupan lahan. Pertama, kita akan men-subset data tutupan lahan yang nonhutan, kemudian mengonversi fitur poligon ke raster sehingga fitur nonhutan memiliki nilai 1 dan hutan bernilai NA. Kita men-subset nonhutan, bukan hutan, karena perintah distance mengukur jarak dari suatu petak raster yang memiliki nilai ke kotak raster terdekat yang bernilai NA.

# Memanggil data
lulc <- readOGR("Input Data/lulc_bbs_2000_2019_natural_human_bbsnp.shp")

# Melihat 13 kategori tutupan lahan
sort(unique(lulc$LULC_2019))

# Kategori yang hutan
hutan <- c("01. Hutan", "02. Hutan mangrove")

# Subset nonhutan, ! artinya inversi
nonhutan_2019 <- subset(lulc, !(LULC_2019 %in% hutan))

# Memberi nilai 1 untuk fitur nonhutan
nonhutan_2019$nonhutan <- 1

# Konversi vektor ke raster
# Area nonhutan akan bernilai 1, sesuai field="hutan"
# Selain itu, bernilai NA
nonhutan_2019_raster <- raster::rasterize(x=nonhutan_2019, y=bbstemp,
                                          field="nonhutan")

# Menghitung jarak ke tepi hutan
nonhutan_2019_dist <- distance(nonhutan_2019_raster)

# Memotong area TNBBS dan buffer saja
dis <- mask(nonhutan_2019_dist, bbsbuffer)

# Mengekspor ke format .asc
writeRaster(dis,"Predictors/res250m_distance_to_forest_edge_2019.asc")

Uji multicollinearity

Sampai di sini, kita sudah memiliki lima raster lingkungan yang akan dipakai sebagai kovariat/prediktor dalam pemodelan distribusi spesies, yaitu elevasi ele, kemiringan lahan slo, keterjalan tapak rou, NDVI ndv, dan jarak ke tepi hutan dis.

# Gabungkan prediktor dalam satu objek `preds`
preds <- stack(ele, slo, rou, ndv, dis)

# Rename komponen 'preds' supaya tidak kepanjangan saat di-plot
names(preds) <- c("ele", "slo", "rou", "ndv", "dis")

# Visualisasi prediktor
plot(preds)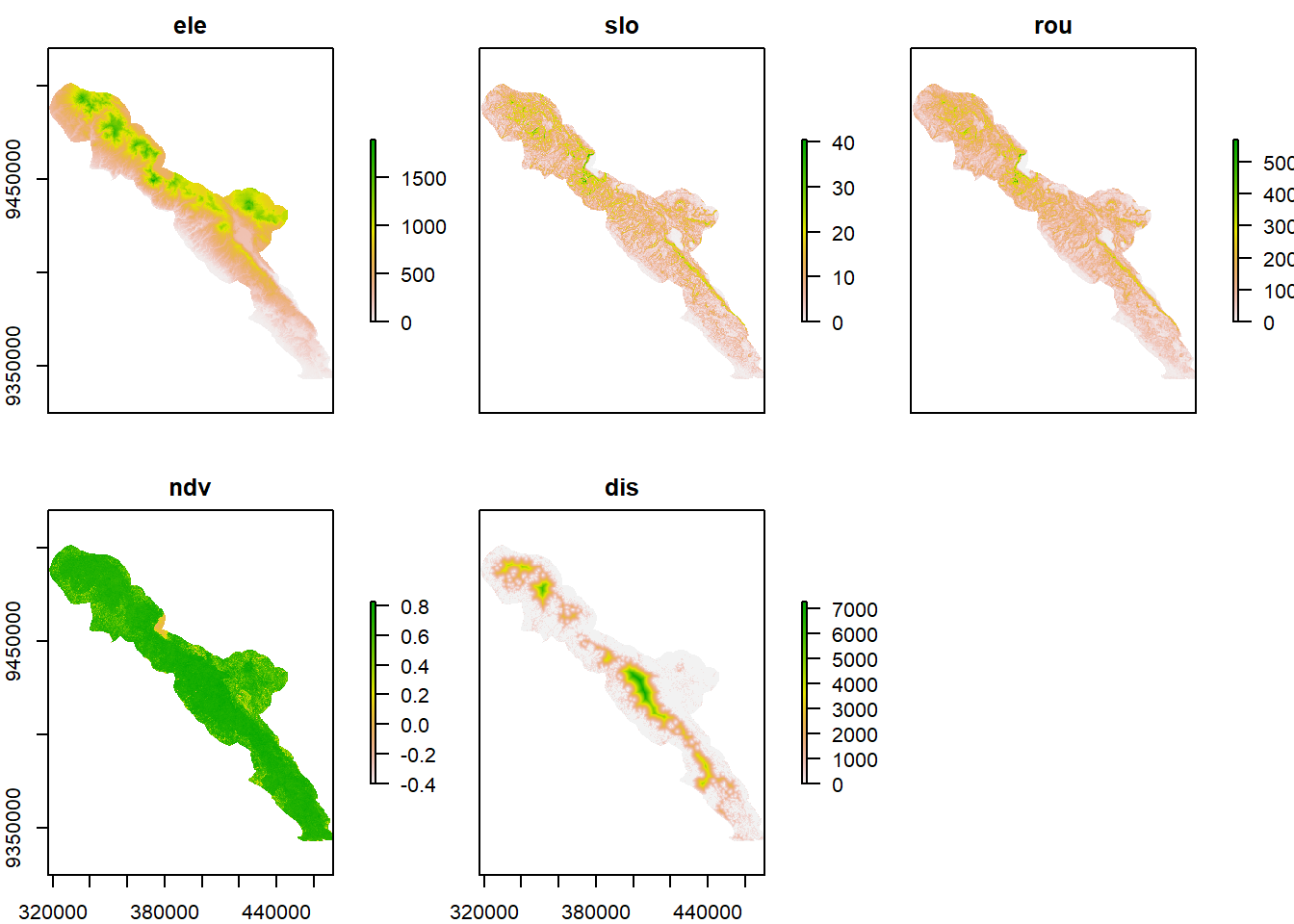

Selanjutnya, kita akan melakukan uji multicollinearity untuk mengetahui apakah ada variabel lingkungan yang saling berkorelasi. Dalam pemodelan distribusi spesies, sebaiknya kita tidak menggunakan variabel lingkungan yang saling berkorelasi karena akan mengaburkan hubungan antara variabel lingkungan dengan keberadaan spesies.

Misalnya, keberadaan spesies owa dipengaruhi oleh tutupan tajuk pohon yang tinggi karena owa hanya dapat bergerak di pepohonan. Sementara itu, tutupan tajuk berkorelasi negatif dengan tutupan tumbuhan bawah (understory). Jika kita menggunakan kedua variabel lingkungan dalam model, pengaruh tutupan tajuk pohon dapat tidak muncul karena ada variabel lain yang berkorelasi dengannya dalam model, yaitu tutupan tumbuhan bawah.

Kita akan menggunakan perintah layerStats untuk melakukan uji korelasi Pearson antara kelima prediktor.

corr_pred <- layerStats(preds, stat = "pearson", na.rm = TRUE)
corr_pred

$`pearson correlation coefficient`
           ele       slo       rou        ndv       dis
ele 1.00000000 0.4310828 0.4654733 0.05230923 0.1728235
slo 0.43108280 1.0000000 0.9442662 0.24583976 0.1272130
rou 0.46547333 0.9442662 1.0000000 0.28565051 0.1507951
ndv 0.05230923 0.2458398 0.2856505 1.00000000 0.3231587
dis 0.17282349 0.1272130 0.1507951 0.32315870 1.0000000

$mean
        ele         slo         rou         ndv         dis 
554.2617195   7.4218407  97.0944594   0.6806674 752.5917050

Tidak ada ketentuan saklek untuk menentukan tinggi atau tidaknya korelasi. Batas yang biasanya digunakan adalah |r|>0,6 atau |r|>0,7, tergantung acuan dan kepercayaan masing-masing.

Berdasarkan hasil uji di atas, terlihat bahwa kelerangan dan keterjalan berkorelasi tinggi (0,94) sehingga kita hanya akan menggunakan salah satunya dalam pemodelan. Menentukan variabel mana yang dipilih juga tidak ada ketentuan khusus. Kita bisa menggunakan pertimbangan ekologis, yaitu berdasarkan pengetahuan kita tentang ekologi spesies, variabel mana yang lebih memberikan pengaruh secara langsung. Atau, bisa juga kita gunakan keduanya dalam pemodelan yang terpisah, tetapi tentunya akan memakan waktu yang lebih banyak. Untuk tujuan latihan ini, kita akan menggunakan kemiringan lereng dan tidak menggunakan keterjalan tapak.

Metode 1: Maxent

Persiapan Data

Data yang dibutuhkan untuk pemodelan menggunakan Maxent adalah data keberadaan spesies (presence only) dan variabel lingkungan dalam format raster yang telah kita buat di bagian sebelumnya. Data keberadaan spesies disimpan dalam format .CSV yang terdiri dari 3 kolom: nama spesies, koordinat X, dan koordinat Y. Dalam satu kali run, kita dapat memodelkan lebih dari satu spesies. Sistem koordinat data spesies dan lingkungan harus sama, misalnya keduanya UTM atau keduanya geographic CRS. Berikut adalah contoh data keberadaan spesies dalam CRS UTM 48S.

Spesies	X	Y
Tragulus kanchil	406523	9416378
Tragulus kanchil	407969	9415929
Tragulus kanchil	412237	9415765
Tragulus kanchil	414739	9414233
Tragulus kanchil	418183	9414547
Tragulus napu	405355	9411438
Tragulus napu	408062	9412467
Tragulus napu	411137	9412834
Tragulus napu	414458	9411927
Tragulus napu	417974	9412469

Kita akan membuat fail .csv untuk input Maxent dari data camera trap. Karena data temuan spesies dan koordinat kamera berada pada sheet yang terpisah, kita perlu menggabungkan keduanya terlebih dahulu.

library(tidyverse);library(readxl)

# Data spesies
spdata <- read_excel("Input Data/DATABASE - BBS_TIGER_SURVEY_2019.xlsx",
                     sheet="Image") %>%
  dplyr::filter(`Genus Species` == "Mydaus javanensis") %>% 
  dplyr::select(`Genus Species`, `Location ID`)
spdata

# A tibble: 275 x 2
   `Genus Species`   `Location ID`
   <chr>             <chr>        
 1 Mydaus javanensis IDN-108-L0001
 2 Mydaus javanensis IDN-108-L0001
 3 Mydaus javanensis IDN-108-L0001
 4 Mydaus javanensis IDN-108-L0001
 5 Mydaus javanensis IDN-108-L0001
 6 Mydaus javanensis IDN-108-L0001
 7 Mydaus javanensis IDN-108-L0001
 8 Mydaus javanensis IDN-108-L0001
 9 Mydaus javanensis IDN-108-L0001
10 Mydaus javanensis IDN-108-L0001
# ... with 265 more rows

# Data lokasi
locdata <- read_excel("Input Data/DATABASE - BBS_TIGER_SURVEY_2019.xlsx",
                     sheet="Deployment") %>% 
  dplyr::select(`Location ID`, X, Y) %>% 
  distinct()

locdata

# A tibble: 65 x 3
   `Location ID`       X       Y
   <chr>           <dbl>   <dbl>
 1 IDN-108-L0001 410043. 9420108
 2 IDN-108-L0002 411656. 9420620
 3 IDN-108-L0003 403964. 9417453
 4 IDN-108-L0004 405670. 9418788
 5 IDN-108-L0005 408496. 9417530
 6 IDN-108-L0006 411770. 9417906
 7 IDN-108-L0007 414715. 9417847
 8 IDN-108-L0008 402775  9416319
 9 IDN-108-L0009 406523  9416378
10 IDN-108-L0010 407969. 9415929
# ... with 55 more rows

# Menggabungkan data temuan spesies dan lokasi
inputdat <- left_join(spdata, locdata) %>% 
  distinct() %>% # menghilangkan data duplikasi
  dplyr::select(-`Location ID`) # menghapus kolom Location ID
  
# Mengekspor tabel sebagai fail .csv
write.csv(inputdat, "maxent_input_file.csv", row.names = F)

Pemodelan

Untuk pemodelan menggunakan Maxent, kita dapat menggunakan perangkat lunak Maxent atau R. Tutorial lengkap penggunaan Maxent dapat diperoleh dari tautan berikut https://www.amnh.org/content/download/141371/2285439/file/LinC3_SpeciesDistModeling_Ex.pdf. Pada modul pelatihan ini, hanya dibahas penggunaan Maxent menggunakan perangkat lunak standalone karena parameter yang dapat diubah lebih lengkap, misalnya feature types, menambakan bias file, regularization, dan sebagainya.

Setelah mengunduh dan mamasang Maxent, jalankan Maxent dengan mengeklik fail bertipe Batch File. Kemudian, akan tampil jendela Maxent seperti gambar di bawah ini.

Komponen utama yang perlu di-assign

1. Data keberadaan spesies

Masukkan data keberadaan spesies dengan mengeklik tombol Browse pada bagian Samples. Pilih fail .csv yang berisi keberadaan spesies, lalu Open. Daftar spesies yang ada di spreadsheet tersebut akan muncul. Jika ada lebih dari satu spesies, kita bisa memilih apakah kita akan memodelkan semua spesies sekaligus atau hanya beberapa dengan mengubah tanda centang di samping nama spesies.

2. Prediktor

Klik Browse di bagian Environmental layers, kemudian pilih folder tempat kita menyimpan fail raster prediktor. Setelah itu, akan muncul daftar fail raster yang ada di folder tersebut dan secara otomatis tercentang semua, tetapi bisa kita ubah secara manual untuk mengikutsertakan atau tidak mengikutsertakan prediktor. Secara otomatis, Maxent akan menentukan tipe data prediktor sebagai variabel Continuous yang tampak di sebelah kanan nama prediktor. Jika ada prediktor yang kategorikal (misalnya tipe tutupan lahan), kita perlu secara manual mengubahnya menjadi Categorical.

Setelah menentukan data keberadaan spesies dan prediktor, centang Create response curves, Make pictures of predictions, dan Do jackknife to measure variable importance. Kemudian kita bisa langsung mengeklik tombol Run di bawah kiri untuk menjalankan Maxent.

Selain komponen-komponen utama di atas, ada beberapa pilihan yang dapat kita ubah untuk mengoptimalkan pemodelan Maxent.

Komponen tambahan

1. Features

Features merupakan fungsi yang digunakan untuk memodelkan hubungan prediktor lingkungan dengan spesies, yaitu linear, quadratic, product, threshold, hinge, dan auto features. By default, pilihan yang aktif adalah auto features sehingga hasil pemodelan dapat mencakup kurva respon yang kompleks. Namun, hal ini dapat menyebabkan overfitting. Jika kita menginginkan model yang lebih general dan secara ekologis lebih “masuk akal”, kita dapat memilih beberapa fitur saja.

Saya pribadi biasanya akan mencoba auto features terlebih dahulu dan jika terdapat kurva respon yang terlalu kompleks, saya akan mencoba lagi dengan hanya memilih linear, quadratic, dan product features.

Dalam beberapa kondisi, mungkin threshold dan hinge features masuk akal secara ekologi. Misalnya, kesesuaian habitat dapat berkurang pada habitat dengan persentase tajuk hingga 70%, tetapi di bawah itu, habitat tersebut sama sekali tidak bisa dihuni siamang dan tidak mungkin ada siamang di situ (nilai kesesuaian habitat langsung drop ke nilai 0).

2. Regularization multiplier

Selain mengubah feature types, kita dapat mengurangi kecenderungan overfitting dengan mengubah regularization multiplier. Angka yang dimasukkan sebagai multiplier diperoleh dengan coba-coba. Pertama, kita menjalankan Maxent dengan default multiplier dahulu. Jika kurva respon terlalu kompleks dan mungkin tidak masuk akal secara ekologi, kita dapat menggunakan multiplier yang lebih besar. Kemudian, hasilnya kita bandingkan.

3. Sampling bias

Walaupun Maxent disebut sebagai metode pemodelan yang hanya menggunakan data presence, sebenarnya Maxent menggunakan titik-titik background, yaitu lokasi (by default maksimal 10.000 titik acak) di permukaan spasial lanskap di mana presence/absence tidak diukur dan mengasumsikan bahwa seluruh lokasi di lanskap disampel secara seimbang.

Konsekuensi hal ini adalah kondisi habitat di mana spesies “mungkin” ada, tetapi tidak disurvei, dapat diduga sebagai habitat tidak sesuai karena terdapat data background di tempat tersebut yang tidak ada temuan spesies.

Sebagai contoh, lokasi titik camera trap di IPZ berkisar antara 160-940 mdpl, sedangkan elevasi seluruh lanskap TNBBS + 5 km buffer berkisar antara 0 hingga 1906 mdpl (lihat gambar di bawah ini). Oleh karena itu, kita tidak memiliki rekaman spesies dari kisaran elevasi 940-1906 mdpl dan Maxent akan menganggap elevasi ini merupakan habitat yang tidak sesuai bagi spesies.

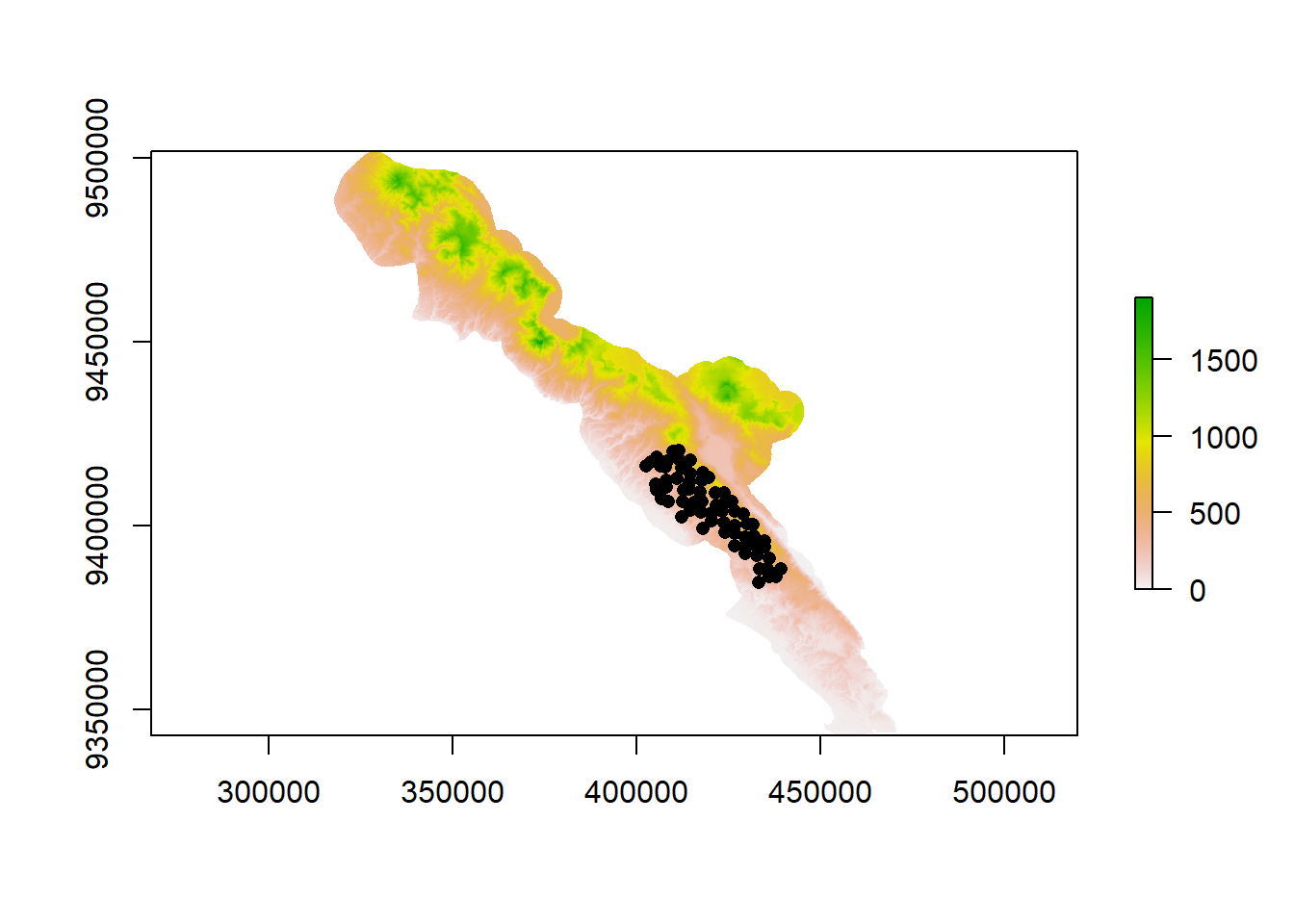
Salah satu cara untuk mengatasi hal ini adalah menggunakan bias file, yaitu fail raster yang merepresentasikan upaya survei relatif di seluruh lanskap. Raster tersebut diberi nilai nonzero antara 0,… (upaya rendah) hingga 1 (upaya tinggi). Jika data keberadaan spesies berasal dari survei camera trap, bias file dapat dibuat dengan memberikan nilai 1 untuk sel raster di sekitar lokasi pemasangan camera trap dan nilai desimal yang kecil (misalnya 0,1) untuk area yang tidak disurvei. “Di sekitar lokasi camera trap” artinya adalah area dalam radius tertentu di sekitar camera trap dan penentuan radius ini bersifat arbitrary. Hasil dari menggunakan bias file adalah titik background tidak dibuat secara acak di seluruh lanskap, melainkan lebih banyak di area yang nilai upaya survei relatifnya lebih tinggi.

Untuk latihan ini, kita akan menggunakan radius 1,5 km (setengah dari 3 km) karena lokasi kamera di IPZ TNBBS ditentukan menggunakan petak 3 km x 3 km.

# Membuat data spasial lokasi kamera
loc_sp <- SpatialPoints(coords=locdata[,c("X","Y")], proj4string=utm48s)

# Membuat buffer 1,5 km
locbuf <- buffer(loc_sp, width=1500)
plot(locbuf);plot(loc_sp, add=T)

# Convert ke raster 
# (area survei otomatis diberi nilai 1, yang tidak disurvei bernilai NA)
locras <- raster::rasterize(locbuf, bbstemp)

# Mengganti nilai raster
# Area survei tetap 1
# Yang tidak disurvei (NA) jadi 0,1
ganti <- data.frame(by = c(1,NA),which= c(1,0.1))
locras2 <- raster::subs(locras, ganti,by=1,which=2)
plot(locras2)

Raster yang dihasilkan mencakup seluruh extent area studi sehingga perlu kita potong dengan vektor area study bbsbuffer.

# Memotong dengan bbsbuffer
bias_file <- mask(locras2, bbsbuffer)
plot(bias_file)

# Mengekspor ke dalam format .asc
writeRaster(bias_file, "bias_file_ipz.asc")

Untuk menggunakan bias file, klik Settings >> Advances. Pada bagian bias file, klik Browse, lalu pilih raster bias file.

Berikut adalah perbandingan peta prediksi distribusi Mydaus javanensis tanpa dan dengan bias file (tipe replikasi crossvalidate, 10 replikasi, dan pengaturan lainnya default).

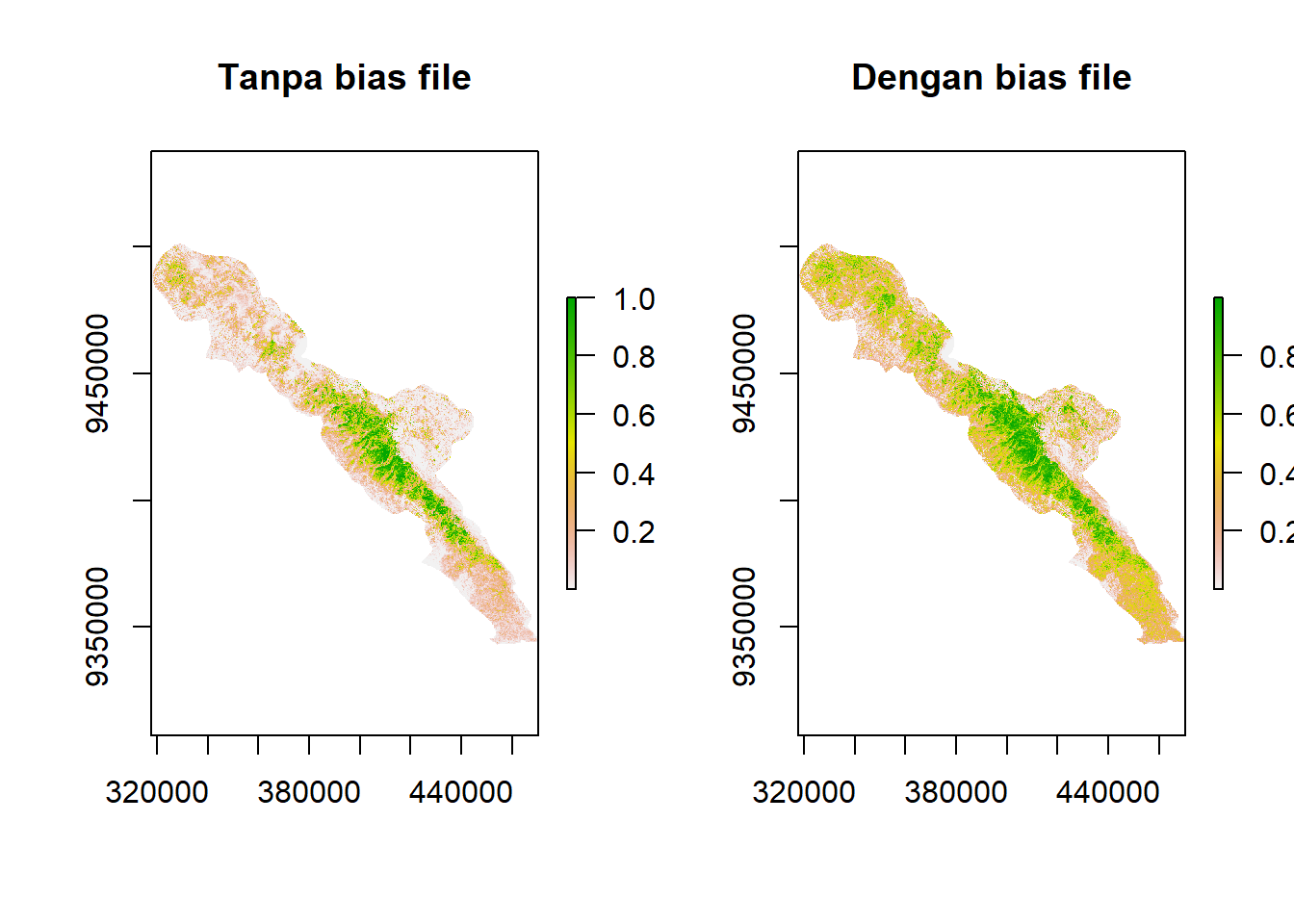
Terlihat bahwa hasil prediksi dengan menggunakan bias file memiliki area dengan kesesuaian habitat tinggi yang lebih luas daripada tanpa bias file. Tanpa bias file, prediksi habitat sesuai akan cenderung hanya berada di sekitar lokasi satwa tersebut diobservasi.

Berikut adalah beberapa bahan bacaan penting untuk mendalami penggunaan Maxent:

Phillips et al. 2017. Opening the black box: an open-source release of Maxent. https://doi.org/10.1111/ecog.03049- Elith et al. 2011. A statistical explanation of MaxEnt for ecologists. https://doi.org/10.1111/j.1472-4642.2010.00725.x
Radosavljevic & Anderson. 2014. Making better Maxent models of species distributions: complexity, overfitting, and evaluation. https://doi.org/10.1111/jbi.12227
Merow et al. 2013. A practical guide to MaxEnt for modeling species distributions: what it does, and why inputs and settings matter. https://doi.org/10.1111/j.1600-0587.2013.07872.x
Phillips et al. 2006. Maximum entropy modeling of species geographic distributions. https://doi.org/10.1016/j.ecolmodel.2005.03.026
Phillips et al. 2004. A maximum entropy approach to species distribution modeling. https://doi.org/10.1145/1015330.1015412

Hasil Maxent

Hasil Maxent dapat dilihat pada fail HTML di folder untuk menyimpan keluaran. Setiap keluaran disertai dengan penjelasan sehingga keluaran dapat dimengerti. Berikut adalah beberapa keluaran penting yang perlu dilaporkan jika melakukan prediksi distribusi satwa menggunakan Maxent.

1. Kurva AUC

Kurva ROC (receiver operator characteristic) Maxent merupakan kurva yang menunjukkan performa model dalam mengklasifikasi keberadaan spesies. AUC (area under the ROC curve) merupakan pengukuran kemampuan model untuk membedakan kategori data. Semakin tinggi AUC, semakin baik kemampuan model dalam membedakan keberadaan spesies. Nilai AUC dapat berkisar antara 0 hingga 1. Nilai mendekati 0 berarti bahwa model memprediksi semua data presence sebagai absence dan sebaliknya; nilai mendekati 1 berarti bahwa model dapat membedakan dengan baik keberadaan spesies. AUC pada model Maxent biasanya berkisar antara 0,5 hingga 1. Nilai 0,5 berarti bahwa model tidak lebih baik daripada model random dalam memprediksi keberadaan spesies. Nilai AUC yang dianggap baik adalah jika > 0,7. Pada gambar di bawah, nilai AUC model adalah 0,872 sehingga model dapat dianggap baik.

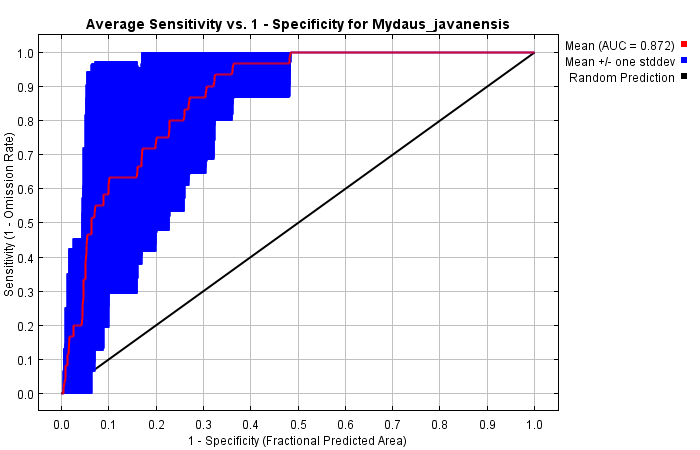
Namun, perlu diingat bahwa nilai AUC dapat bernilai tinggi jika spesies yang dimodelkan memiliki area distribusi yang sempit relatif terhadap seluruh area studi. Hal ini tidak selalu berarti model tersebut baik (Maxent Tutorial, 2017)

2. Kurva respon

Kurva respon memperlihatkan bagaimana hubungan antara nilai prediktor lingkungan dengan prediksi keberadaan spesies/kesesuaian habitat: apakah hubungannya bersifat linier, kuadratik, kombinasi beberapa fungsi, atau yang lain?

Pada halaman keluaran Maxent, terdapat dua macam kurva respon, yaitu kurva respon marginal dan kurva respon yang hanya dibuat menggunakan satu variabel. Bentuk kurva respon antara kedua tipe tersebut dapat berbeda, terutama jika terdapat korelasi antarvariabel. Baca keterangan pada halaman HTML keluaran untuk keterangan lebih lanjut.

3. Prediktor apa yang paling penting?

Terdapat dua cara untuk menentukan variabel lingkungan yang paling penting terhadap distribusi spesies, yaitu 1) tabel kontribusi dan permutasi dan 2) Jackknife of training and test gain and AUC. Kita berharap variabel yang paling penting berdasarkan kedua cara tersebut sama, tetapi sering kali hasilnya dapat berbeda. Jika berbeda, saya pribadi cenderung memilih menggunakan hasil dari Jackknife of trianing and test gain karena menunjukkan peningkatan performa model saat menggunakan satu variabel tertentu dan penurunan performa model saat variabel tersebut tidak digunakan (baca keterangan di halaman HTML dan Maxent Tutorial untuk penjelasan lebih rinci).

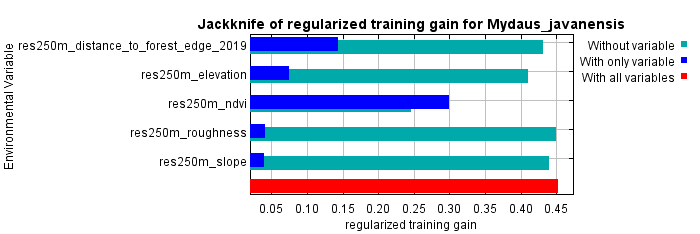
Jika suatu variabel memiliki gain yang rendah, kurva respon variabel tersebut dapat diabaikan. Jadi, yang penting dijelaskan dalam laporan adalah pola kurva respon variabel lingkungan yang memiliki gain tinggi saja.

4. Peta prediksi distribusi spesies

Hasil dari prediksi distribusi spesies adalah indeks yang berkisar antara 0 hingga 1. Indeks ini dapat diinterpretasikan sebagai probabilitas keberadaan spesies atau indeks kesesuaian habitat. Semakin mendekati 1, semakin tinggi prediksi keberadaan spesies/prediksi kesesuaian habitat, dan sebaliknya.

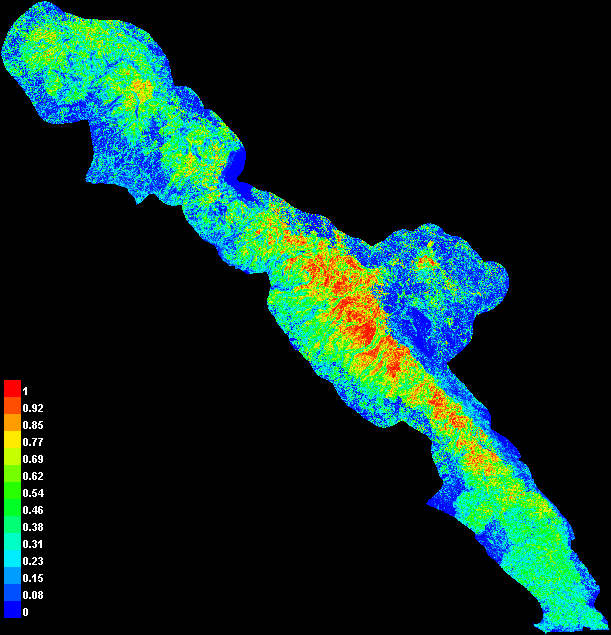
Di dalam halaman HTML keluaran Maxent, terdapat peta dalam format PNG. Peta dalam format raster ASC juga dihasilkan Maxent di folder keluaran.

Metode 2: Generalized Linear Model

Persiapan Data

Data keberadaan spesies yang dibutuhkan untuk GLM dalah data presence/absence. Jika spesies di temukan di suatu lokasi survei, lokasi tersebut diberi nilai 1. Jika tidak ada spesies di lokasi tersebut, diberi nilai 0. Kolom spesies bisa lebih dari satu jika kita akan menganalisis multispesies. Berikut contoh data input GLM.

ID Lokasi	spA	spB
CT001	1	0
CT002	0	1
CT003	0	1
CT004	1	1
CT005	1	1

Salah satu kekurangan dari metode GLM adalah kita tidak dapat memastikan ketidakberadaan spesies. Misalnya, kita survei menggunakan camera trap di 10 lokasi dan spesies target ditemukan di 4 lokasi. Di 6 lokasi lainnya, bukan berarti spesies tersebut benar-benar tidak ada. Bisa jadi spesies target ada, hanya tidak terdeteksi. Masalah tentang probabilitas deteksi ini akan dibahas dalam pemodelan okupansi. Namun, asumsi dalam kerangka kerja GLM adalah data non-detection dianggap sebagai true absence.

Data yang akan kita gunakan di latihan ini adalah data rekaman spesies dari camera trap dan kita akan memodelkan distribusi Mydaus javanensis, tetapi sebagai contoh multispesies, kita akan men-subset juga Paguma larvata.

library(tidyverse);library(readxl)

spdata <- read_excel("Input Data/DATABASE - BBS_TIGER_SURVEY_2019.xlsx",
                     sheet="Image") %>%
  dplyr::filter(`Genus Species` %in% c("Mydaus javanensis",
                                       "Paguma larvata")) 
spdata

# A tibble: 696 x 21
   `Deployment ID` `Location ID`  Grid Camera `Image Id` Location `Photo Type`
   <chr>           <chr>         <dbl> <chr>  <chr>      <chr>    <chr>       
 1 IDN-108-D0011   IDN-108-L0001     1 A      GRID1A-19~ PHOTOS_~ Animal      
 2 IDN-108-D0011   IDN-108-L0001     1 A      GRID1A-19~ PHOTOS_~ Animal      
 3 IDN-108-D0011   IDN-108-L0001     1 A      GRID1A-19~ PHOTOS_~ Animal      
 4 IDN-108-D0011   IDN-108-L0001     1 A      GRID1A-19~ PHOTOS_~ Animal      
 5 IDN-108-D0011   IDN-108-L0001     1 A      GRID1A-19~ PHOTOS_~ Animal      
 6 IDN-108-D0011   IDN-108-L0001     1 A      GRID1A-19~ PHOTOS_~ Animal      
 7 IDN-108-D0011   IDN-108-L0001     1 A      GRID1A-19~ PHOTOS_~ Animal      
 8 IDN-108-D0011   IDN-108-L0001     1 A      GRID1A-19~ PHOTOS_~ Animal      
 9 IDN-108-D0011   IDN-108-L0001     1 A      GRID1A-19~ PHOTOS_~ Animal      
10 IDN-108-D0011   IDN-108-L0001     1 A      GRID1A-19~ PHOTOS_~ Animal      
# ... with 686 more rows, and 14 more variables: `Photo Type Identified
#   by` <chr>, `Genus Species` <chr>, `IUCN Identification Number` <dbl>,
#   `Date_Time Captured` <dttm>, Time <dbl>, Age <chr>, Sex <chr>, `Tiger
#   ID` <chr>, `Tiger ID (Refer to ID Convention)` <lgl>, Count <dbl>, `Animal
#   recognizable (Y/N, blank)` <lgl>, `Individual Animal notes` <lgl>,
#   `Independent Event` <dbl>, Keterangan <chr>

Data spesies ini perlu kita modifikasi terlebih dahulu sebelum digabungkan dengan data koordinat lokasi.

spdata <- spdata %>% 
  dplyr::select(`Location ID`,`Genus Species`) %>% # memilih kolom lokasi dan spesies saja
  mutate(presence=1) %>% # assign nilai 1 untuk presence
  distinct() %>% # hilangkan duplikasi temuan di lokasi yang sama
  spread(key=`Genus Species`,value=presence, fill=0) # membuat matriks lokasi X spesies 

spdata

# A tibble: 39 x 3
   `Location ID` `Mydaus javanensis` `Paguma larvata`
   <chr>                       <dbl>            <dbl>
 1 IDN-108-L0001                   1                0
 2 IDN-108-L0002                   1                1
 3 IDN-108-L0005                   1                1
 4 IDN-108-L0007                   1                1
 5 IDN-108-L0008                   1                1
 6 IDN-108-L0009                   1                1
 7 IDN-108-L0010                   1                0
 8 IDN-108-L0011                   1                0
 9 IDN-108-L0012                   1                0
10 IDN-108-L0013                   0                1
# ... with 29 more rows

Kemudian, kita akan memanggil data lokasi kamera dan koordinat untuk menggabungkan data spesies dengan data lokasi kamera. Kita hanya akan menggunakan tiga kolom yang akan dipilih dengan perintah select. Data lokasi kamera yang digunakan berasal dari survei harimau sehingga dua kamera dipasang berhadapan di satu koordinat/lokasi. Oleh karena itu, kita akan menghilangkan data duplikat kamera dengan perintah distinct.

locdata <- read_excel("Input Data/DATABASE - BBS_TIGER_SURVEY_2019.xlsx",
                     sheet="Deployment") %>% 
  dplyr::select(`Location ID`, X, Y) %>% 
  distinct()

locdata

# A tibble: 65 x 3
   `Location ID`       X       Y
   <chr>           <dbl>   <dbl>
 1 IDN-108-L0001 410043. 9420108
 2 IDN-108-L0002 411656. 9420620
 3 IDN-108-L0003 403964. 9417453
 4 IDN-108-L0004 405670. 9418788
 5 IDN-108-L0005 408496. 9417530
 6 IDN-108-L0006 411770. 9417906
 7 IDN-108-L0007 414715. 9417847
 8 IDN-108-L0008 402775  9416319
 9 IDN-108-L0009 406523  9416378
10 IDN-108-L0010 407969. 9415929
# ... with 55 more rows

Gabungkan data lokasi kamera dan data keberadaan spesies.

sploc <- left_join(locdata,spdata) %>%
  replace(is.na(.), 0) # mengganti NA dengan 0

sploc

# A tibble: 65 x 5
   `Location ID`       X       Y `Mydaus javanensis` `Paguma larvata`
   <chr>           <dbl>   <dbl>               <dbl>            <dbl>
 1 IDN-108-L0001 410043. 9420108                   1                0
 2 IDN-108-L0002 411656. 9420620                   1                1
 3 IDN-108-L0003 403964. 9417453                   0                0
 4 IDN-108-L0004 405670. 9418788                   0                0
 5 IDN-108-L0005 408496. 9417530                   1                1
 6 IDN-108-L0006 411770. 9417906                   0                0
 7 IDN-108-L0007 414715. 9417847                   1                1
 8 IDN-108-L0008 402775  9416319                   1                1
 9 IDN-108-L0009 406523  9416378                   1                1
10 IDN-108-L0010 407969. 9415929                   1                0
# ... with 55 more rows

Langkah selanjutnya adalah mengekstrak nilai variabel lingkungan di lokasi kamera. Kita akan kembali menggunakan package spasial. Aktifkan package terlebih dahulu jika belum: library(sp);library(raster).

library(sp);library(raster)

# CRS yang digunakan
utm48s <- CRS("+proj=utm +zone=48 +south +datum=WGS84 +units=m +no_defs")

# Membuat data spasial titik CT
locspatial <- SpatialPoints(coords=locdata[,c("X","Y")], proj4string=utm48s)

# Memanggil raster variabel lingkungan
# (raster ini dibuat pada bagian Pemrosesan Variabel Lingkungan)
ele <- raster("Predictors/res250m_elevation.asc")
slo <- raster("Predictors/res250m_slope.asc")
rou <- raster("Predictors/res250m_roughness.asc")
ndv <- raster("Predictors/res250m_ndvi.asc")
dis <- raster("Predictors/res250m_distance_to_forest_edge_2019.asc")
# Menggabungkan kelima prediktor menjadi satu raster stack
preds <- stack(ele, slo, rou, ndv, dis)
# Rename komponen objek preds
names(preds) <- c("ele", "slo", "rou", "ndv", "dis")

# Mengekstrak variabel lingkungan
predvalues <- raster::extract(preds, locspatial)

# Menggabungkan nilai prediktor dengan data temuan spesies
glmdata <- cbind(sploc, predvalues)

Pemodelan

Untuk mem-fit model, kita menggunakan perintah glm(...). Karena variabel respon merupakan data biner (presence/absence), family yang digunakan adalah "binomial". Khusus untuk variabel elevasi, kita akan mengikutsertakan fungsi kuadratik untuk memperhitungkan kemungkinan bahwa spesies memiliki preferensi ketinggian tertentu.

fullmodel <- glm(`Mydaus javanensis` ~ ele+I(ele^2)+slo+ndv+dis,
                 data=glmdata, family="binomial")
summary(fullmodel)


Call:
glm(formula = `Mydaus javanensis` ~ ele + I(ele^2) + slo + ndv + 
    dis, family = "binomial", data = glmdata)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.4169  -0.9430  -0.6907   1.1224   2.0915  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)
(Intercept)  3.210e+00  1.252e+01   0.256    0.798
ele          7.343e-03  1.020e-02   0.720    0.472
I(ele^2)    -3.042e-06  8.646e-06  -0.352    0.725
slo         -9.366e-03  7.169e-02  -0.131    0.896
ndv         -9.308e+00  1.695e+01  -0.549    0.583
dis          2.216e-04  2.436e-04   0.910    0.363

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 86.616  on 64  degrees of freedom
Residual deviance: 78.823  on 59  degrees of freedom
AIC: 90.823

Number of Fisher Scoring iterations: 4

Hal terpenting yang perlu dilihat dari hasil di atas adalah tabel Coefficients. Terdapat lima kolom pada bagian tersebut, yaitu kolom nama prediktor, estimasi beta koefisien prediktor, standard error, z-value, dan p-value (Pr(>|z|)). Baris pertama pada tabel tersebut adalah intercept persamaan linier, yaitu nilai prediksi jika seluruh prediktor bernilai 0. Baris kedua dan seterusnya adalah prediktor yang kita modelkan.

Kolom Estimate menunjukkan estimasi beta koefisien masing-masing prediktor. Jika nilai Estimate negatif, semakin tinggi nilai prediktor, semakin rendah probabilitas keberadaan spesies. Sebaliknya, jika nilai Estimate positif, semakin tinggi nilai prediktor, semakin tinggi juga probabilitas keberadaan spesies. Namun, kita perlu mengetahui apakah hubungan tersebut signifikan dengan melihat kolom p-value.

Jika p-value < 0.05, beta koefisien prediktor tersebut signifikan, atau dengan kata lain, prediktor tersebut berpengaruh signifikan terhadap estimasi probabilitas keberadaan spesies. Di contoh ini, tidak ada prediktor yang signifikan pada full model.

Seleksi model

Langkah selanjutnya setelah fit full model adalah mendapatkan model parsimonious dengan metode step wise. Model parsimonious adalah model paling sederhana (prediktor paling sedikit) yang memiliki kemampuan prediksi paling besar. Indeks yang digunakan untuk mengevaluasi model parsimonious adalah Akaike Information Criterion (AIC). Semakin kecil nilai AIC, model tersebut semakin parsimonious.

stepmod <- step(fullmodel)

Start:  AIC=90.82
`Mydaus javanensis` ~ ele + I(ele^2) + slo + ndv + dis

           Df Deviance    AIC
- slo       1   78.840 88.840
- I(ele^2)  1   78.948 88.948
- ndv       1   79.126 89.126
- ele       1   79.359 89.359
- dis       1   79.662 89.662
<none>          78.823 90.823

Step:  AIC=88.84
`Mydaus javanensis` ~ ele + I(ele^2) + ndv + dis

           Df Deviance    AIC
- I(ele^2)  1   78.953 86.953
- ndv       1   79.131 87.131
- ele       1   79.359 87.359
- dis       1   79.792 87.792
<none>          78.840 88.840

Step:  AIC=86.95
`Mydaus javanensis` ~ ele + ndv + dis

       Df Deviance    AIC
- ndv   1   79.198 85.198
- dis   1   80.705 86.705
<none>      78.953 86.953
- ele   1   85.158 91.158

Step:  AIC=85.2
`Mydaus javanensis` ~ ele + dis

       Df Deviance    AIC
- dis   1   81.162 85.162
<none>      79.198 85.198
- ele   1   85.191 89.191

Step:  AIC=85.16
`Mydaus javanensis` ~ ele

       Df Deviance    AIC
<none>      81.162 85.162
- ele   1   86.616 88.616

Regresi step wise bekerja dengan cara mengeliminasi prediktor satu per satu, lalu membandingkan dengan satu sama lain dan model lengkap. Jika model yang salah satu prediktornya dieliminasi memiliki nilai AIC lebih rendah dari model lengkap, model tersebut dipilih untuk langkah selanjutnya. Hal tersebut terjadi bertahap hingga diperoleh model dengan AIC terendah.

Pada data kita, pada tahap pertama, model tanpa prediktor slo (kelerengan) memiliki nilai AIC terendah (88.840) jika dibandingkan dengan model tanpa salah satu variabel lain dan model lengkap (<none> pada tabel hasil step wise).

Pada langkah kedua, “model lengkap”-nya adalah model tanpa prediktor slope, yaitu Mydaus javanensis ~ ele + I(ele^2) + ndv + dis, kemudian prediktor dieliminasi satu per satu. Hasilnya adalah model tanpa prediktor I(ele^2) (fungsi kuadratik elevasi), memiliki AIC terendah (86.953).

Setelah langkah ketiga dan seterusnya, diketahui bahwa model Mydaus javanensis ~ ele sebagai model terbaik dengan nilai AIC = 85.162.

Untuk melihat koefisien prediktor dan nilai signifikansinya, jalankan perintah berikut.

summary(stepmod)


Call:
glm(formula = `Mydaus javanensis` ~ ele, family = "binomial", 
    data = glmdata)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.5476  -0.9216  -0.7323   1.1922   1.8166  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)   
(Intercept) -2.252667   0.856369  -2.630  0.00853 **
ele          0.003289   0.001476   2.228  0.02588 * 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 86.616  on 64  degrees of freedom
Residual deviance: 81.162  on 63  degrees of freedom
AIC: 85.162

Number of Fisher Scoring iterations: 4

Dari hasil di atas, dapat disimpulkan bahwa prediktor yang berkontribusi signifikan dalam menentukan keberadaan Mydaus javanensis adalah elevasi dengan koefisien 0,003289 (SE = 0,001476; p-value = 0,02588).

Membuat kurva respon

Untuk melihat hubungan antara prediktor dengan prediksi probabilitas keberadaan spesies, kita perlu membuat kurva respon.

Elevasi

# Data baru untuk response curve
newDat<-data.frame(ele=seq(min(glmdata$ele),max(glmdata$ele),length=100)) 
# Prediksi
pred <- predict(stepmod, newdata=newDat, type="response", se.fit=TRUE)

# Menggabungkan estimasi dan newDat
glmpred <- cbind(as.data.frame(pred), newDat)

# Plot
glmpred %>% 
  ggplot(aes(x = ele, y = fit)) +
  geom_ribbon(aes(ymin = fit-se.fit, ymax = fit+se.fit), 
              alpha = 0.5, linetype = "dashed") +
  geom_path(size = 1) +
  labs(x = "Elevasi", y = "Probabilitas keberadaan") +
  theme_classic() +
  coord_cartesian(ylim = c(0,1))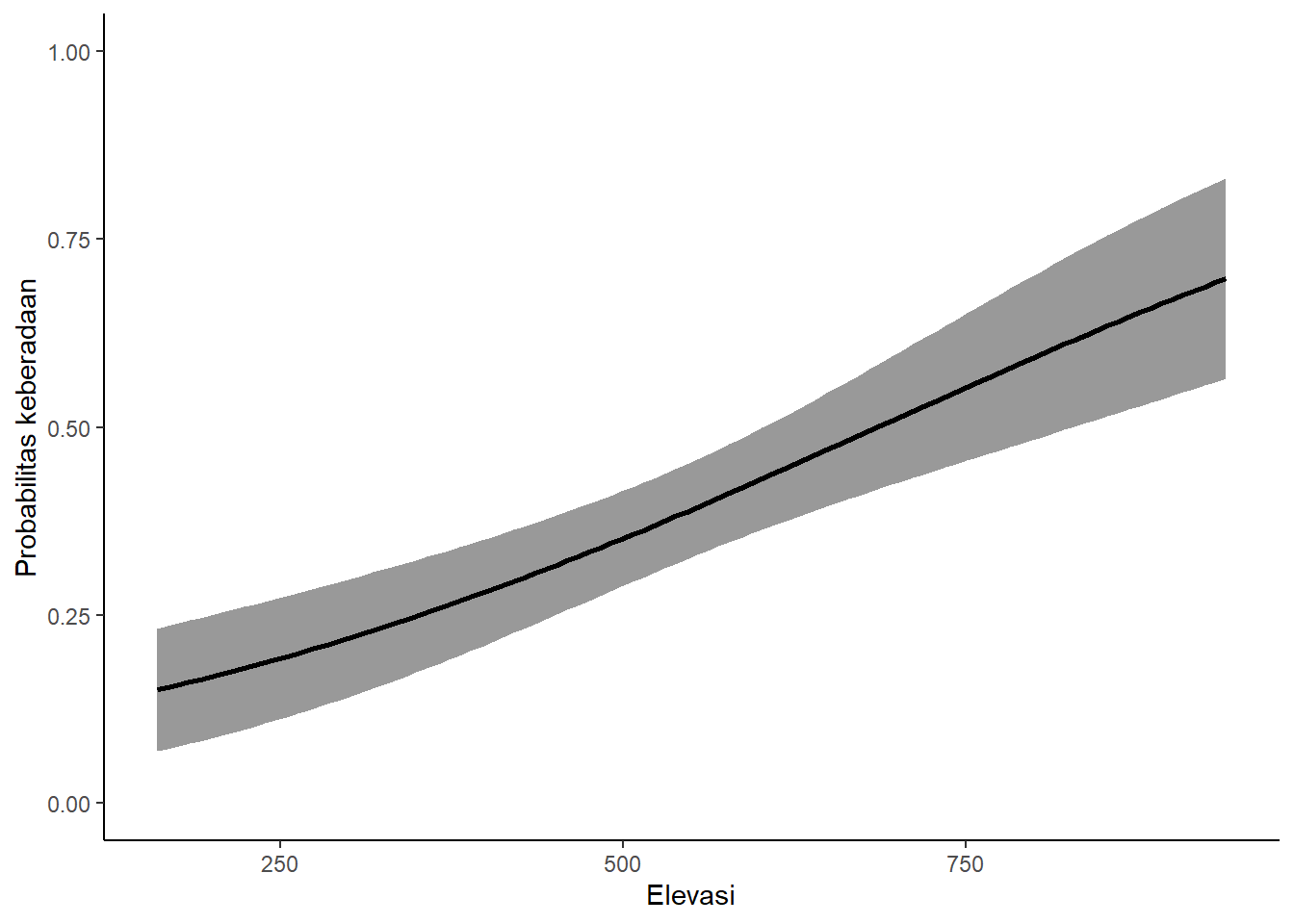

Prediksi spasial

Setelah didapatkan model terbaik (model parsimonious), kita akan menggunakannya untuk memprediksi keberadaan Mydaus javanensis di area studi kita dengan perintah predict. Karena kita menggunakan GLM yang variabel responnya biner (1/0), kita perlu mengonversi keluaran dari predict menjadi angka probabilitas yang berkisar antara 0 dan 1 dengan perintah calc dan fungsi plogis.

# Kalkulasi prediksi keberadaan spsies di lanskap studi
probpredict <- predict(preds, stepmod, fun=predict)

# Mengubah nilai prediksi menjadi skala 0-1 dengan fungsi plogis
probglm <- calc(probpredict, fun = function(x){plogis(x)})

# Menampilkan peta prediksi
plot(probglm)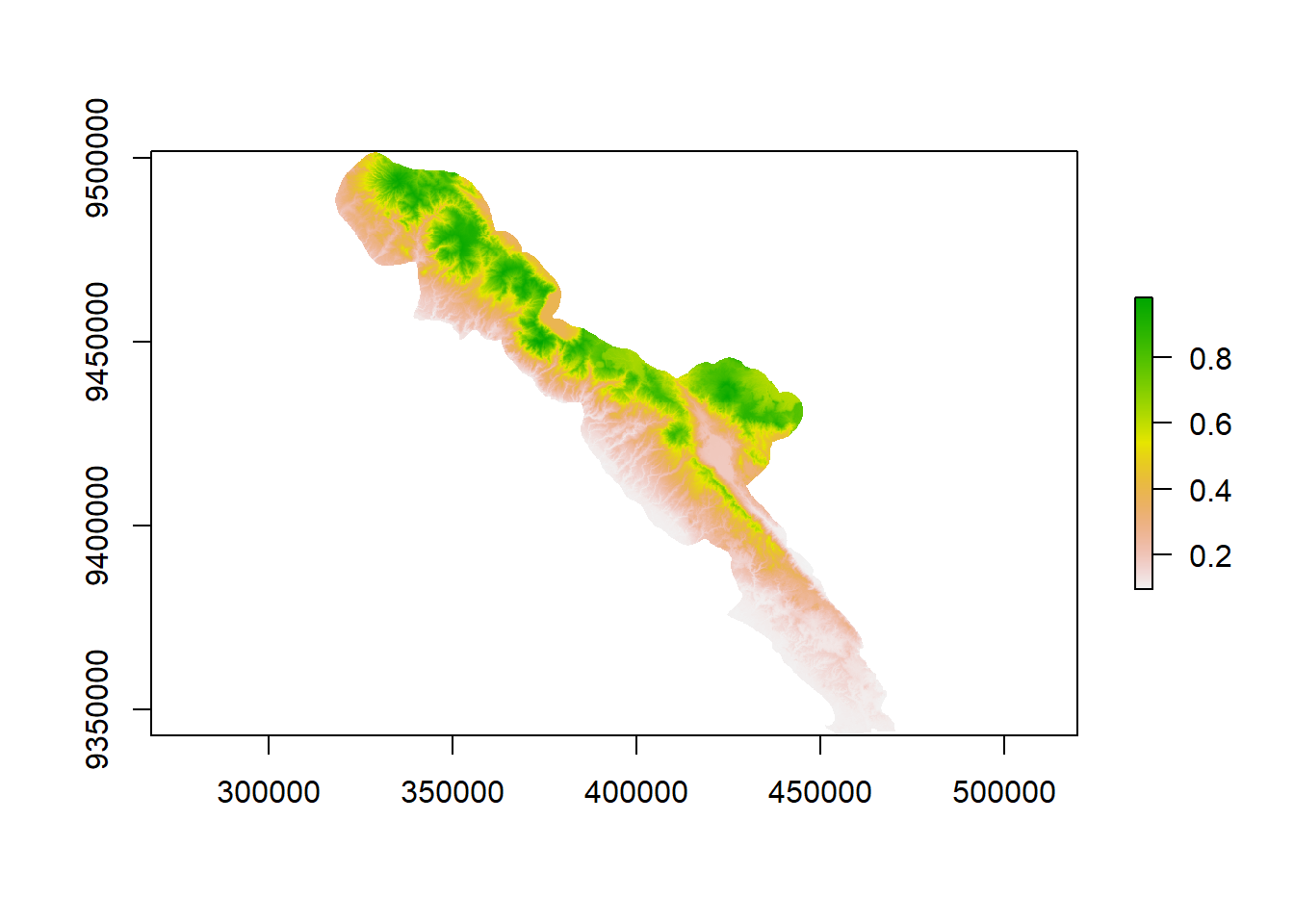

Kita juga bisa mengekspor peta prediksi probabilitas keberadaan Mydaus javanensis ke dalam format raster.

writeRaster(probglm, filename="GLM_Mydaus_javanensis.tif")

Metode 3: Occupancy modeling

Pemodelan okupansi merupakan pemodelan proporsi area yang dihuni oleh satwa dengan mempertimbangkan probabilitas deteksi satwa. Jika kita menemukan satwa di suatu unit sampel (misalnya grid), hal itu berarti satwa tersebut menempati unit sampel tersebut. Namun, jika kita tidak menemukan satwa (nondeteksi), hal itu dapat berarti:
- satwa menempati unit sampel, tetapi tidak terdeteksi oleh observer, atau - satwa benar-benar tidak menempati unit sampel (absence).

Berbeda dengan GLM yang mengasumsikan nondeteksi sebagai absence, pemodelan okupansi menggunakan pengambilan sampel berulang (repeated sampling) di setiap unit sampel untuk menghitung probabilitas deteksi $p$. Replikasi pengambilan sampel dapat berupa pengulangan spasial, misalnya pada survei okupansi harimau se-Pulau Sumatera (SWTS), atau pengulangan temporal, misalnya pada survei camera trap, seperti yang akan kita lakukan pada latihan ini.

Pemodelan okupansi merupakan pemodelan berhierarki karena terdapat dua parameter yang diestimasi, yaitu probabilitas okupansi $$ dan probabilitas deteksi $p$.

Persiapan Data

Untuk melakukan pemodelan okupansi, kita perlu membuat matriks deteksi spesies. Baris matriks merupakan lokasi survei dan kolom matriks berisi hasil pengambilan sampel berulang. Setiap pengambilan sampel disebut sampling occasion. Kita akan menggunakan package camtrapR untuk membuat matriks deteksi spesies, tidyverse untuk memodifikasi bentuk data, dan readxl untuk membaca fail .XLSX.

Pertama, kita akan memanggil data rekaman spesies.

library(tidyverse);library(readxl);library(camtrapR)

# Data spesies
spdata <- read_excel("Input Data/DATABASE - BBS_TIGER_SURVEY_2019.xlsx",
                     sheet="Image") %>% 
    dplyr::select(LocationID = `Location ID`,
                  Species = `Genus Species`,
                  datetime = `Date_Time Captured`) 

spdata

# A tibble: 122,491 x 3
   LocationID    Species          datetime           
   <chr>         <chr>            <dttm>             
 1 IDN-108-L0001 Argusianus argus 2019-07-02 07:50:01
 2 IDN-108-L0001 Argusianus argus 2019-07-02 07:50:02
 3 IDN-108-L0001 Argusianus argus 2019-07-05 11:15:47
 4 IDN-108-L0001 Argusianus argus 2019-07-05 11:15:48
 5 IDN-108-L0001 Argusianus argus 2019-07-05 11:15:49
 6 IDN-108-L0001 Argusianus argus 2019-07-14 06:56:02
 7 IDN-108-L0001 Argusianus argus 2019-07-14 11:55:21
 8 IDN-108-L0001 Argusianus argus 2019-07-14 11:55:21
 9 IDN-108-L0001 Argusianus argus 2019-07-16 17:40:17
10 IDN-108-L0001 Argusianus argus 2019-07-16 17:40:19
# ... with 122,481 more rows

Kemudian, kita akan memanggil data pemasangan dan pengambilan kamera dan koordinat untuk menggabungkan data spesies dengan data lokasi kamera.

# Data pemasangan dan lokasi kamera
camdata <- read_excel("Input Data/DATABASE - BBS_TIGER_SURVEY_2019.xlsx",
                     sheet="Deployment") %>% 
  dplyr::select(DeploymentID=`Deployment ID`,
                LocationID=`Location ID`,
                X,Y,
                Begin=`Camera Deployment Begin Date`,
                End=`Camera last picture date`) %>% 
  dplyr::filter(!is.na(End)) 
  
camdata

# A tibble: 126 x 6
   DeploymentID LocationID      X      Y Begin               End                
   <chr>        <chr>       <dbl>  <dbl> <dttm>              <dttm>             
 1 IDN-108-D00~ IDN-108-L~ 4.10e5 9.42e6 2019-06-28 00:00:00 2019-11-15 00:00:00
 2 IDN-108-D00~ IDN-108-L~ 4.12e5 9.42e6 2019-06-28 00:00:00 2019-11-15 00:00:00
 3 IDN-108-D00~ IDN-108-L~ 4.12e5 9.42e6 2019-06-28 00:00:00 2019-11-15 00:00:00
 4 IDN-108-D00~ IDN-108-L~ 4.04e5 9.42e6 2019-06-29 00:00:00 2019-11-16 00:00:00
 5 IDN-108-D00~ IDN-108-L~ 4.06e5 9.42e6 2019-06-29 00:00:00 2019-06-29 00:00:00
 6 IDN-108-D00~ IDN-108-L~ 4.06e5 9.42e6 2019-06-29 00:00:00 2019-11-16 00:00:00
 7 IDN-108-D00~ IDN-108-L~ 4.08e5 9.42e6 2019-06-30 00:00:00 2019-11-17 00:00:00
 8 IDN-108-D00~ IDN-108-L~ 4.08e5 9.42e6 2019-06-30 00:00:00 2019-11-17 00:00:00
 9 IDN-108-D00~ IDN-108-L~ 4.12e5 9.42e6 2019-06-27 00:00:00 2019-11-14 00:00:00
10 IDN-108-D00~ IDN-108-L~ 4.12e5 9.42e6 2019-06-27 00:00:00 2019-11-14 00:00:00
# ... with 116 more rows

# Membuat camera operation matrix
CTmatrix <- cameraOperation(CTtable = camdata,
                            stationCol = "LocationID",
                            cameraCol = "DeploymentID",
                            setupCol = "Begin",
                            retrievalCol = "End",
                            hasProblems = FALSE,
                            byCamera = FALSE,
                            allCamsOn = FALSE,
                            camerasIndependent = FALSE,
                            dateFormat = "%Y-%m-%d",
                            writecsv = TRUE,
                            outDir = getwd()
                            )

# Membuat species detection matrix
spdet <- detectionHistory(recordTable = spdata, 
                          species = "Mydaus javanensis",
                          camOp = CTmatrix,
                          stationCol = "LocationID",
                          speciesCol = "Species",
                          recordDateTimeCol = "datetime",
                          recordDateTimeFormat = "%Y-%m-%d %H:%M:%S",
                          occasionLength = 7,
                          minActiveDaysPerOccasion = 4,
                          day1 = "survey",
                          includeEffort = FALSE,
                          scaleEffort = FALSE,
                          occasionStartTime = 0,
                          datesAsOccasionNames = TRUE,
                          timeZone = "Asia/Jakarta",
                          writecsv = F)

# Untuk melihat hasil akhirnya (matriks deteksi)
View(spdet)

Selanjutnya, kita akan mengekstrak nilai variabel lingkungan pada lokasi kamera.

library(sp);library(raster)

# Membuat tabel koordinat kamera
ctloc <- camdata %>% dplyr::select(LocationID, X, Y) %>% distinct() 

# CRS yang digunakan
utm48s <- CRS("+proj=utm +zone=48 +south +datum=WGS84 +units=m +no_defs")

# Mengubah tabel koordinat menjadi data spasial
ct_sp <- SpatialPoints(coords=ctloc[,c("X","Y")], proj4string=utm48s)

# Memanggil raster prediktor
ele <- raster("Predictors/res250m_elevation.asc")
slo <- raster("Predictors/res250m_slope.asc")
rou <- raster("Predictors/res250m_roughness.asc")
ndv <- raster("Predictors/res250m_ndvi.asc")
dis <- raster("Predictors/res250m_distance_to_forest_edge_2019.asc")

# Menggabungkan prediktor lingkungan menjadi satu objek
preds <- stack(ele,slo,rou,ndv,dis)

# Rename komponen prediktor
names(preds) <- c("ele","slo","rou","ndv","dis")

# Mengekstrak nilai prediktor di lokasi kamera
predvalues <- raster::extract(preds, ct_sp) %>% as.data.frame()
 
# Melihat korelasi antarprediktor 
library(PerformanceAnalytics) 
chart.Correlation(predvalues, histogram=TRUE, pch=19)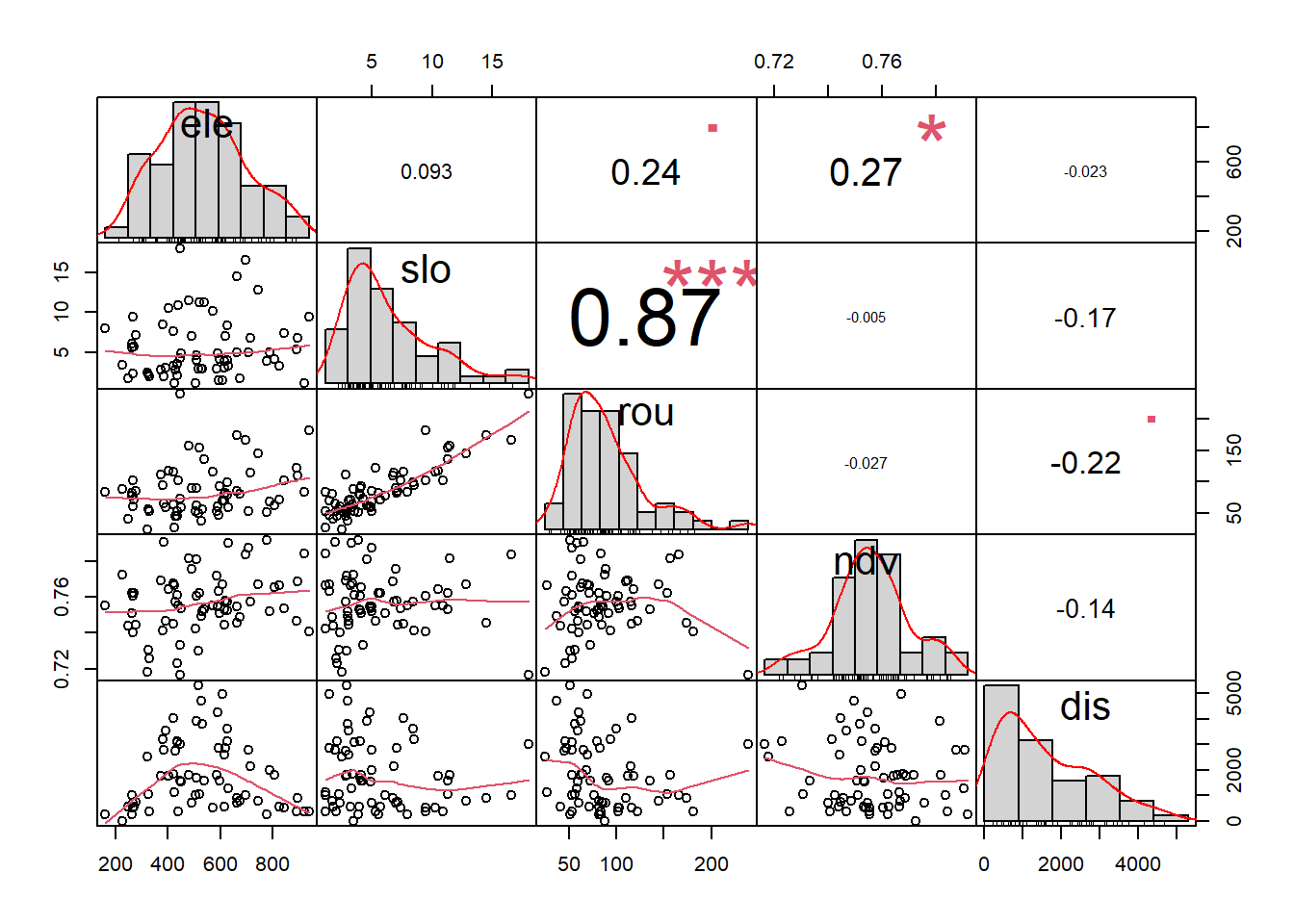

Pemodelan

Package yang digunakan untuk melakukan pemodelan okupansi adalah unmarked. Pasang package tersebut terlebih dahulu jika belum ada.

library(unmarked)

umf <- unmarkedFrameOccu(y = spdet$detection_history, 
                         siteCovs = predvalues)
plot(umf)

Berbeda dengan GLM, biasanya pemodelan okupansi dilakukan dari model konstan terlebih dahulu, kemudian menambahkan prediktor satu per satu dan membandingkan nilai AIC-nya. Namun, sebenarnya kita juga bisa melakukan seleksi model dari model lengkap (full model) dan satu per satu mengeliminasi prediktor. Hal ini dapat dilakukan jika prediktor kita tidak terlalu banyak.

Jika prediktor banyak, tentu akan memakan banyak waktu untuk mencoba seluruh kombinasi model. Alternatif lainnya adalah menyusun beberapa model kandidat yang mencakup kombinasi beberapa prediktor yang memiliki makna ekologis saja.

Dalam contoh latihan ini, kita akan mencoba melakukan pemodelan okupansi dari model konstan dan satu per satu menambahkan prediktor.

Keputusan lainnya yang perlu kita buat adalah apakah kita akan menyusun model kandidat untuk parameter probabilitas okupansi $\psi$ atau probabilitas deteksi $p$ terlebih dahulu? Hal ini juga tergantung aliran kepercayaan masing-masing. Biasanya, saya pribadi akan memodelkan $p$ dahulu dengan $\psi$ konstan. Lalu, jika sudah didapatkan best model untuk $p$, saya akan menyusun model kandidat untuk memodelkan $\psi$.

Pertama, kita akan fit model konstan $p \sim 1 , \psi \sim 1$, lalu menambahkan prediktor NDVI untuk probabilitas deteksi $p$.

# Fit models
mods <- list()

mods$null <- occu(~1 ~1, data = umf)
mods$ndv._ <- occu(~ndv ~1, data = umf)

# Model selection
fitlist <- fitList(fits=mods)
(modSel <- modSel(fitlist, nullmod = 'null'))

      nPars    AIC delta AICwt cumltvWt  Rsq
ndv._     3 464.69  0.00  0.85     0.85 0.08
null      2 468.08  3.40  0.15     1.00 0.00

Pada iterasi pertama, terlihat bahwa model dengan NDVI sebagai prediktor probabilitas deteksi memiliki AIC yang paling rendah sehingga kita akan memakai $p \sim NDVI$ untuk tahap selanjutnya, yaitu mem-fit-kan prediktor untuk parameter $\psi$.

mods$ndv.ele <- occu(~ndv ~ele, data = umf)
mods$ndv.ele2 <- occu(~ndv ~ele+I(ele^2), data = umf)
mods$ndv.slo <- occu(~ndv ~slo, data = umf)
mods$ndv.ndv <- occu(~ndv ~ndv, data = umf)
mods$ndv.dis <- occu(~ndv ~dis, data = umf)

# Model selection
fitlist <- fitList(fits=mods)
(modSel <- modSel(fitlist, nullmod = 'null'))

         nPars    AIC  delta   AICwt cumltvWt      Rsq
ndv.ele      4 460.79   0.00 7.8e-01     0.78    0.160
ndv._        3 464.69   3.89 1.1e-01     0.89    0.080
ndv.ndv      4 466.50   5.71 4.5e-02     0.94    0.082
ndv.slo      4 466.68   5.88 4.1e-02     0.98    0.080
null         2 468.08   7.29 2.0e-02     1.00    0.000
ndv.dis      4 478.04  17.24 1.4e-04     1.00   -0.096
ndv.ele2     5 811.04 350.25 6.9e-77     1.00 -177.532

Pada iterasi kedua, model dengan AIC terendah adalah $p \sim NDVI, \psi \sim elevasi$. Untuk tahap selanjutnya, kita akan menambahkan satu prediktor untuk $\psi$ selain elevasi.

mods$ndv.eleslo <- occu(~ndv ~ele+slo, data = umf)
mods$ndv.elendv <- occu(~ndv ~ele+ndv, data = umf)
mods$ndv.eledis <- occu(~ndv ~ele+dis, data = umf)

# Model selection
fitlist <- fitList(fits=mods)
(modSel <- modSel(fitlist, nullmod = 'null'))

Pada tahap ini, model dengan AIC terendah tetap $p \sim NDVI, \psi \sim elevasi$ sehingga model fitting dihentikan pada tahap ini dan model ini kita anggap model terbaik yang akan digunakan untuk membuat kurva respon dan peta distribusi.

# Best model
bestmod <- mods$ndv.ele
summary(bestmod)


Call:
occu(formula = ~ndv ~ ele, data = umf)

Occupancy (logit-scale):
            Estimate      SE     z P(>|z|)
(Intercept) -2.63821 1.04851 -2.52  0.0119
ele          0.00441 0.00197  2.24  0.0250

Detection (logit-scale):
            Estimate   SE     z P(>|z|)
(Intercept)    -14.0 6.25 -2.24  0.0249
ndv             15.7 8.21  1.92  0.0553

AIC: 460.7946 
Number of sites: 65
optim convergence code: 0
optim iterations: 102 
Bootstrap iterations: 0

Membuat kurva respon

Sama seperti GLM, untuk membuat kurva respon, kita akan membuat data frame baru. Nilai elevasi dibuat berkisar antara nilai minimal dan maksimal data asli, sedangkan untuk prediktor yang lain digunakan nilai rata-rata.

predpsi <- predict(bestmod, type="state")

# Membuat data prediktor yang baru
occu_newdata <- data.frame(ele = seq(min(predvalues$ele),
                                     max(predvalues$ele),by=0.1),
                           slo = mean(predvalues$slo),
                           ndv = mean(predvalues$ndv),
                           dis = mean(predvalues$dis))

occu_toppred <- predict(bestmod, occu_newdata, type="state")
occu_toppred_df <- data.frame(occu_toppred,occu_newdata)

occu_toppred_df %>% 
  ggplot(aes(x = ele, y = Predicted)) +
  geom_ribbon(aes(ymin = lower, ymax = upper), alpha = 0.5, linetype = "dashed") +
  geom_path(size = 1) +
  labs(x = "Elevasi", y = "Probabilitas okupansi") +
  theme_classic() +
  coord_cartesian(ylim = c(0,1))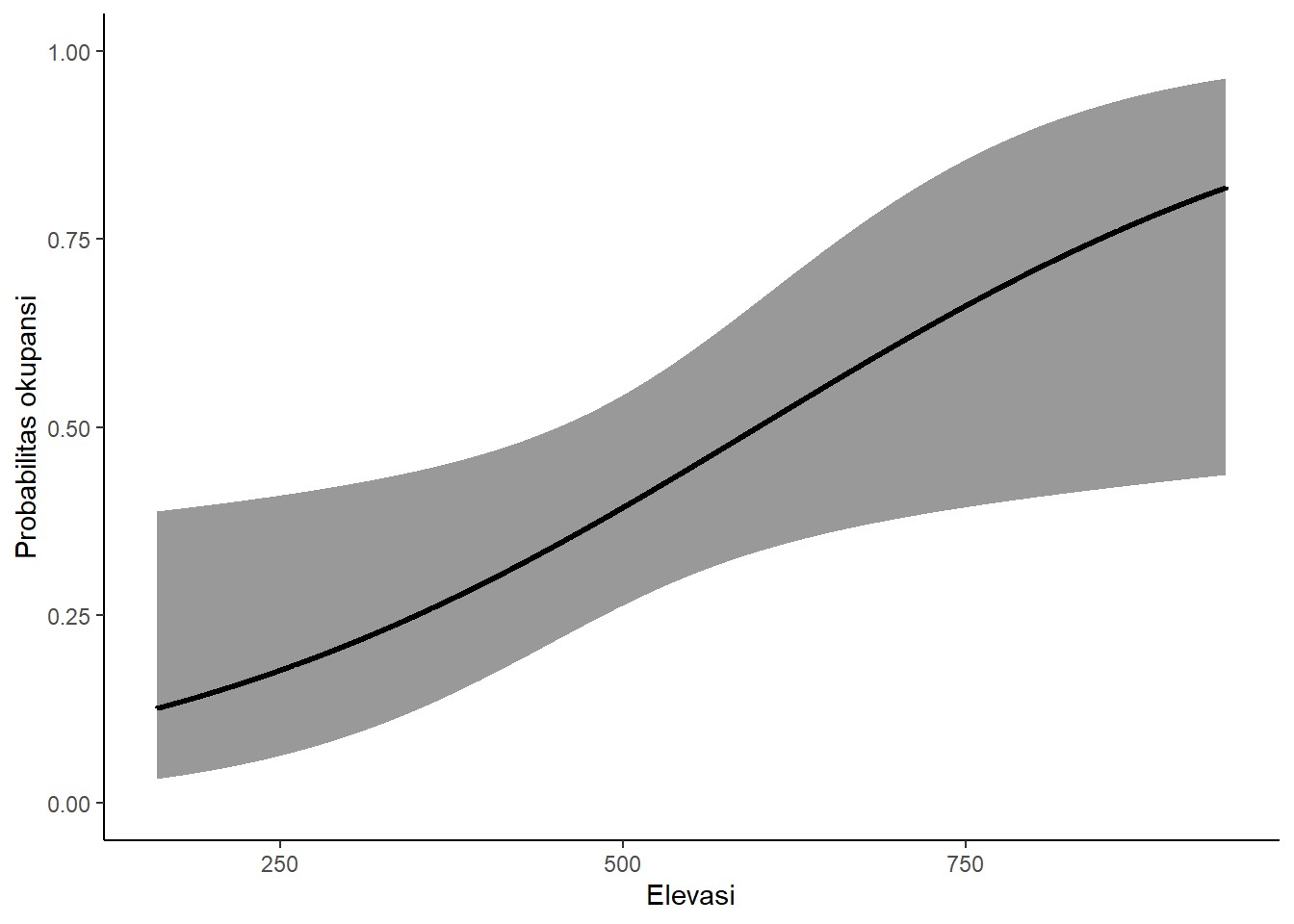

Prediksi spasial

predoccu <- predict(preds, bestmod, type="state")
probocc <- calc(predoccu, fun = function(x){plogis(x)})

plot(probocc)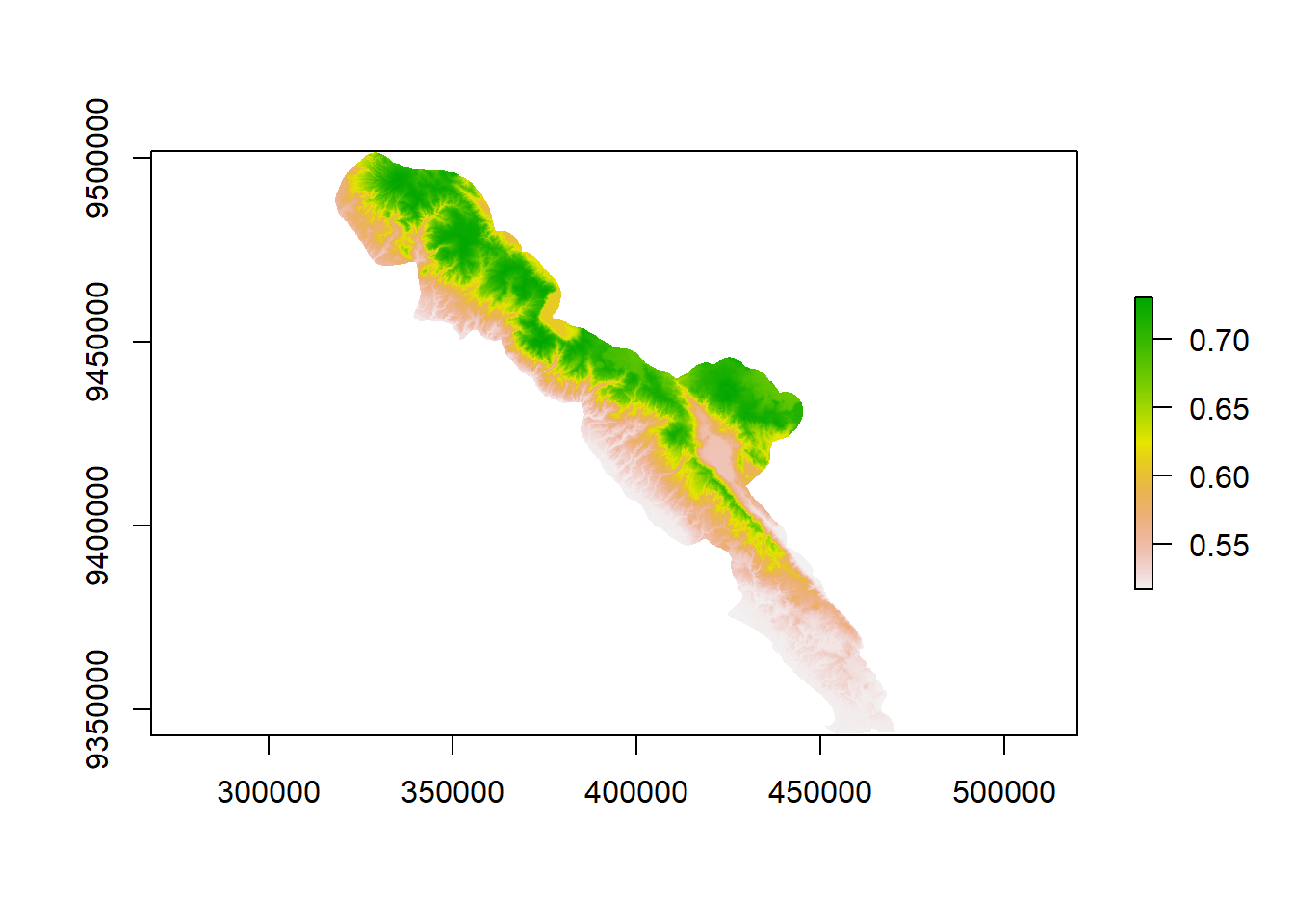

writeRaster(prob_sp, filename="Occupancy_Mydaus_javanensis.tif")

Membandingkan Peta Ketiga Metode

Untuk membandingkan ketiga peta prediksi, kita perlu memanggil peta hasil Maxent terlebih dahulu. Peta tersebut ada di folder keluaran Maxent dan berformat .ASC. Berikut adalah contoh perintah untuk memanggil peta prediksi yang berisi nilai rata-rata dari 10 kali replikasi crossvalidate (nama_spesies_avg.asc). Bisa juga memakai nilai median (nama_spesies_median.asc).

petamaxent <- raster("Output/max_linqua/Mydaus_javanensis_avg.asc")

Kemudian, kita plotkan ketiga petanya berdampingan.

par(mfrow=c(1,3))
plot(petamaxent, main="Maxent")
plot(probglm, main="GLM")
plot(probocc, main="Occupancy")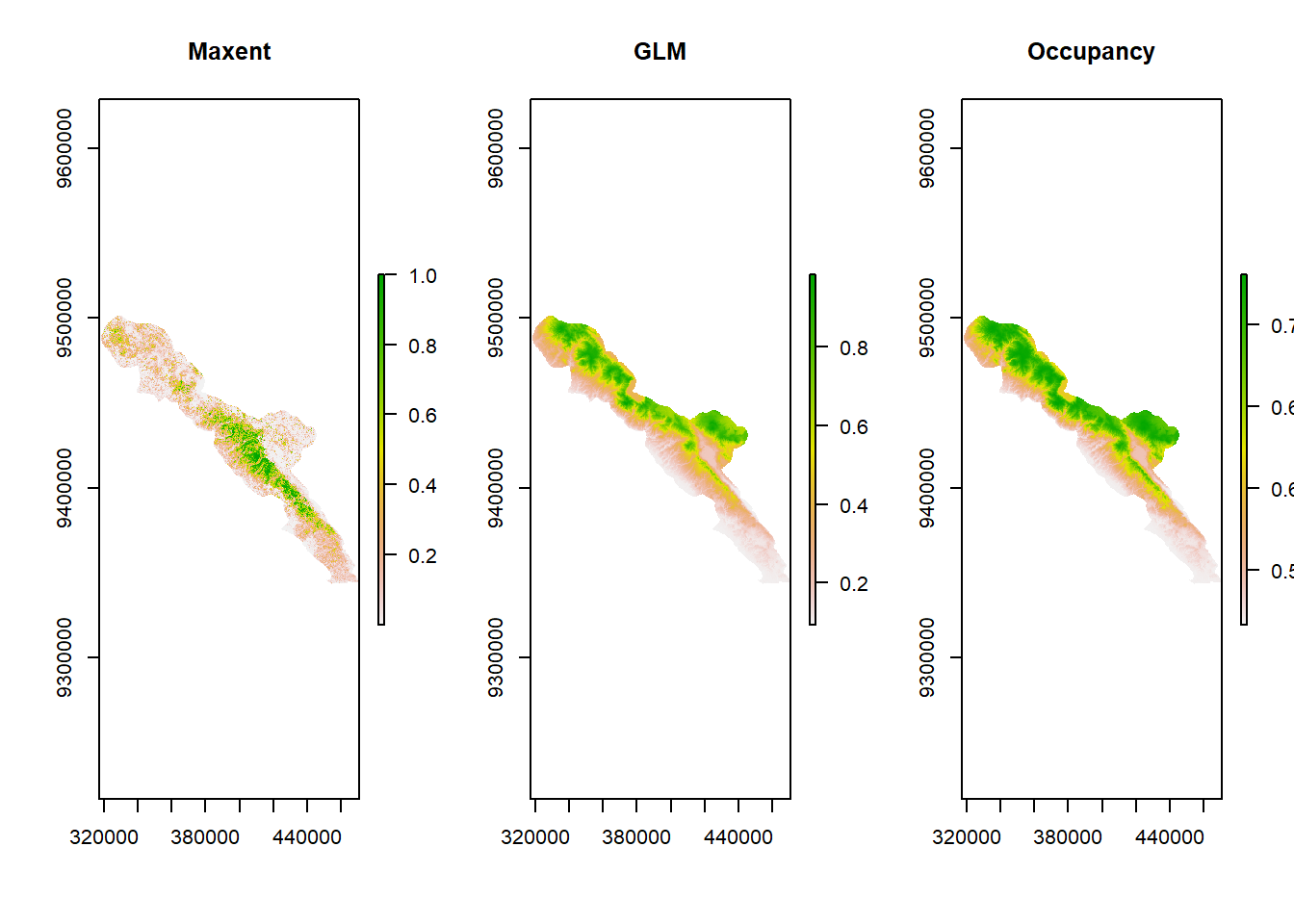

Kira-kira menurut kalian, apa perbedaan antara ketiga metode tersebut?

Model Averaging

Pada contoh GLM dan okupansi di modul ini, kita hanya menggunakan satu model untuk membuat kurva respon dan peta prediksi, yaitu model yang memiliki nilai AIC terendah. Namun, misalnya ada model A yang memiliki nilai AIC = 460,79 dan model B dengan AIC = 460,82. Model A memang memiliki AIC yang lebih rendah, tetapi perbedaannya kecil, yaitu hanya 0,03. Perbedaan nilai AIC disebut “delta AIC”. Jika AIC terlalu kecil, kita bisa bilang performa kedua model tersebut tidak berbeda jauh.

Selain pendekatan best model, ada juga pendekatan model averaging, yaitu merata-ratakan model yang nilai delta AIC-nya tidak jauh berbeda, lalu menggunakan averaged model ini untuk membuat kurva respon dan peta prediksi. Biasanya, threshold yang digunakan adalah delta AIC < 2.

Pada tabel seleksi model okupansi sebelumnya, terlihat bahwa ada tiga model yang delta AIC-nya < 2 sehingga ketiga model ini dirata-ratakan untuk membuat prediksi.

         nPars    AIC  delta   AICwt cumltvWt      Rsq
ndv.ele      4 460.79   0.00 7.8e-01     0.78    0.160
ndv._        3 464.69   3.89 1.1e-01     0.89    0.080
ndv.ndv      4 466.50   5.71 4.5e-02     0.94    0.082
ndv.slo      4 466.68   5.88 4.1e-02     0.98    0.080
null         2 468.08   7.29 2.0e-02     1.00    0.000
ndv.dis      4 478.04  17.24 1.4e-04     1.00   -0.096
ndv.ele2     5 811.04 350.25 6.9e-77     1.00 -177.532

Referensi

Hansen, M. C. C, P V Potapov, R. Moore, M. Hancher, S. A. a Turubanova, A. Tyukavina, D. Thau, et al. 2013. “High-resolution global maps of 21st-century forest cover change.” Science 342 (November): 850–54. https://doi.org/10.1126/science.1244693.

Lubis, M I, S Hussein, H Wandono, and W Marthy. 2018. “Monitoring perubahan tutupan hutan di bentang alam Bukit Barisan Selatan periode 2000-2017.” Bukit Barisan Selatan National Park & WCS Indonesia Program.

Rondinini, Carlo, Moreno Di Marco, Federica Chiozza, Giulia Santulli, Daniele Baisero, Piero Visconti, Michael Hoffmann, et al. 2011. “Global habitat suitability models of terrestrial mammals.” Philosophical Transactions of the Royal Society B: Biological Sciences 366: 2633–41. https://doi.org/10.1098/rstb.2011.0113.

Rondinini, Carlo, Kerrie A. Wilson, Luigi Boitani, Hedley Grantham, and Hugh P. Possingham. 2006. “Tradeoffs of different types of species occurrence data for use in systematic conservation planning.” Ecology Letters 9 (10): 1136–45. https://doi.org/10.1111/j.1461-0248.2006.00970.x.

Daftar Isi

Pemodelan Distribusi Spesies

Oktober 2021

Cakupan Pelatihan

Prasyarat

Pendahuluan

Pemrosesan Variabel Lingkungan

1. Elevasi

2. Kemiringan lahan (slope) dan keterjalan tapak (roughness)

3. NDVI

4. Jarak dari tepi hutan

Uji multicollinearity

Metode 1: Maxent

Persiapan Data

Pemodelan

Komponen utama yang perlu di-assign

1. Data keberadaan spesies

2. Prediktor

Komponen tambahan

1. Features

2. Regularization multiplier

3. Sampling bias

Hasil Maxent

1. Kurva AUC

2. Kurva respon

3. Prediktor apa yang paling penting?

4. Peta prediksi distribusi spesies

Metode 2: Generalized Linear Model

Persiapan Data

Pemodelan

Seleksi model

Membuat kurva respon

Elevasi

Prediksi spasial

Metode 3: Occupancy modeling

Persiapan Data

Pemodelan

Membuat kurva respon

Prediksi spasial

Membandingkan Peta Ketiga Metode

Model Averaging

Referensi